ABC is an isosceles triangle with AB\ =\ AC . Draw AP⊥BC to show that ∠B\ =∠C.
The correct Answer is:∠C
Step by step video solution for ABC is an isosceles triangle with A B"\ "="\ "A C . Draw A P_|_B C to show that /_B"\ "=/_Cdot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
ABC is an isosceles triangle with AB= AC. Draw AP⊥BC to show that ∠B=∠C.
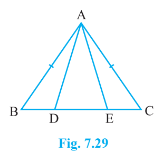
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
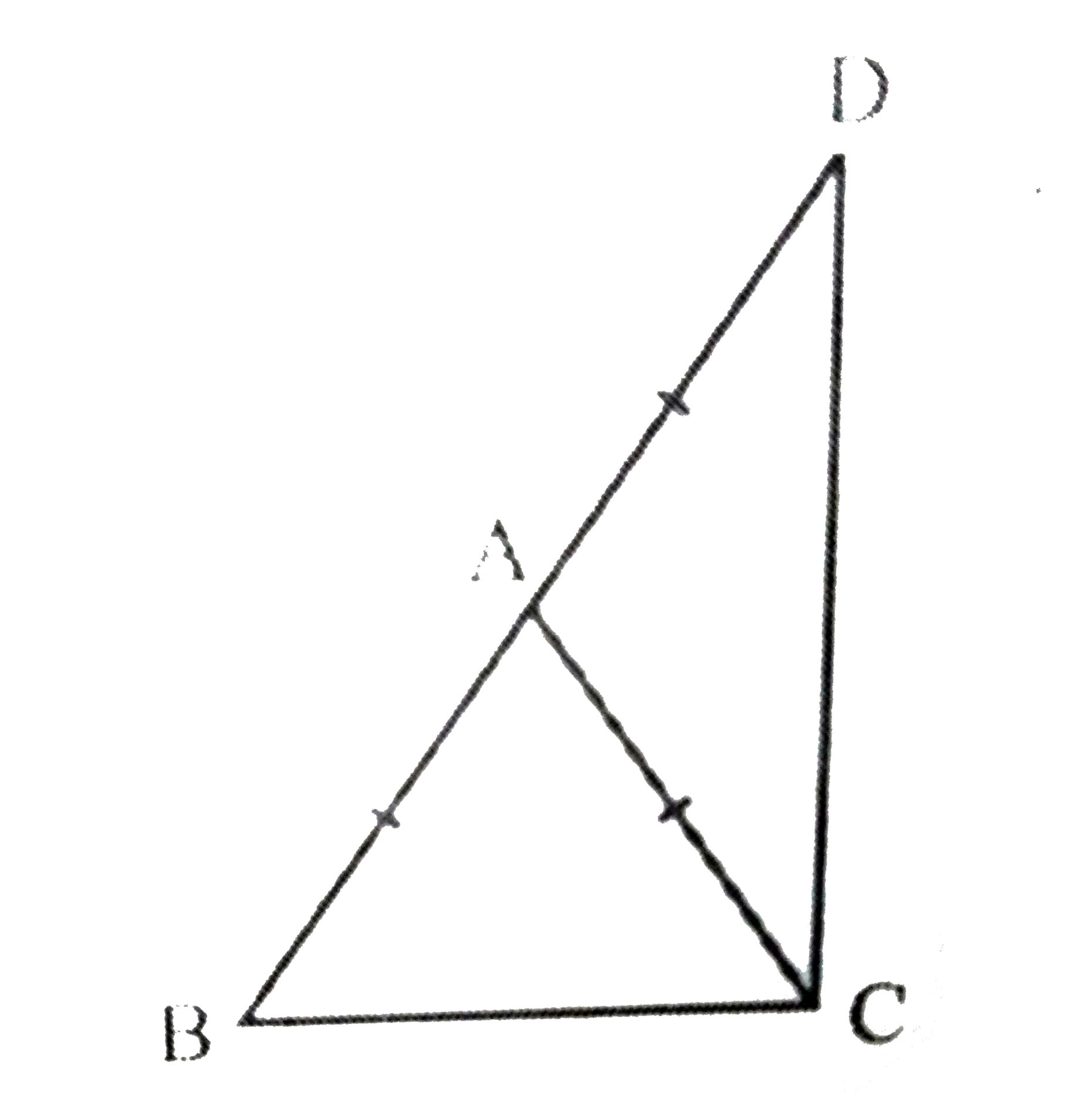
View SolutionΔABC is an isosceles triangle in which AB=AC. Side BA is produced to D such that AD=AB (see Fig. 7.34). Show that ∠BCD is a right angle.
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.

View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.

View SolutionIn an isosceles triangle ABC, with AB=AC, the bisectors of B and C intersect each other at O. Join A to O. Show that :
(i) OB=OC
(ii) AO bisects A
View SolutionLet ABC be an isosceles triangle in which AB=AC If D,E,F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
View SolutionABC is an isosceles triangle inscribed in a circle of radius r. If AB=AC and h is the altitude from A to BC, then triangle ABC has perimeter P=2(√2hr−h2+√2hr) and area A= ____________ and = __________ and also (lim)x→0AP3=____
View SolutionA triangle ABC is an isosceles triangle if any one of the following conditions hold: Altitude AD bisects ∠BAC. Bisector of ∠BAC is perpendicular to the base BC.
View Solution
