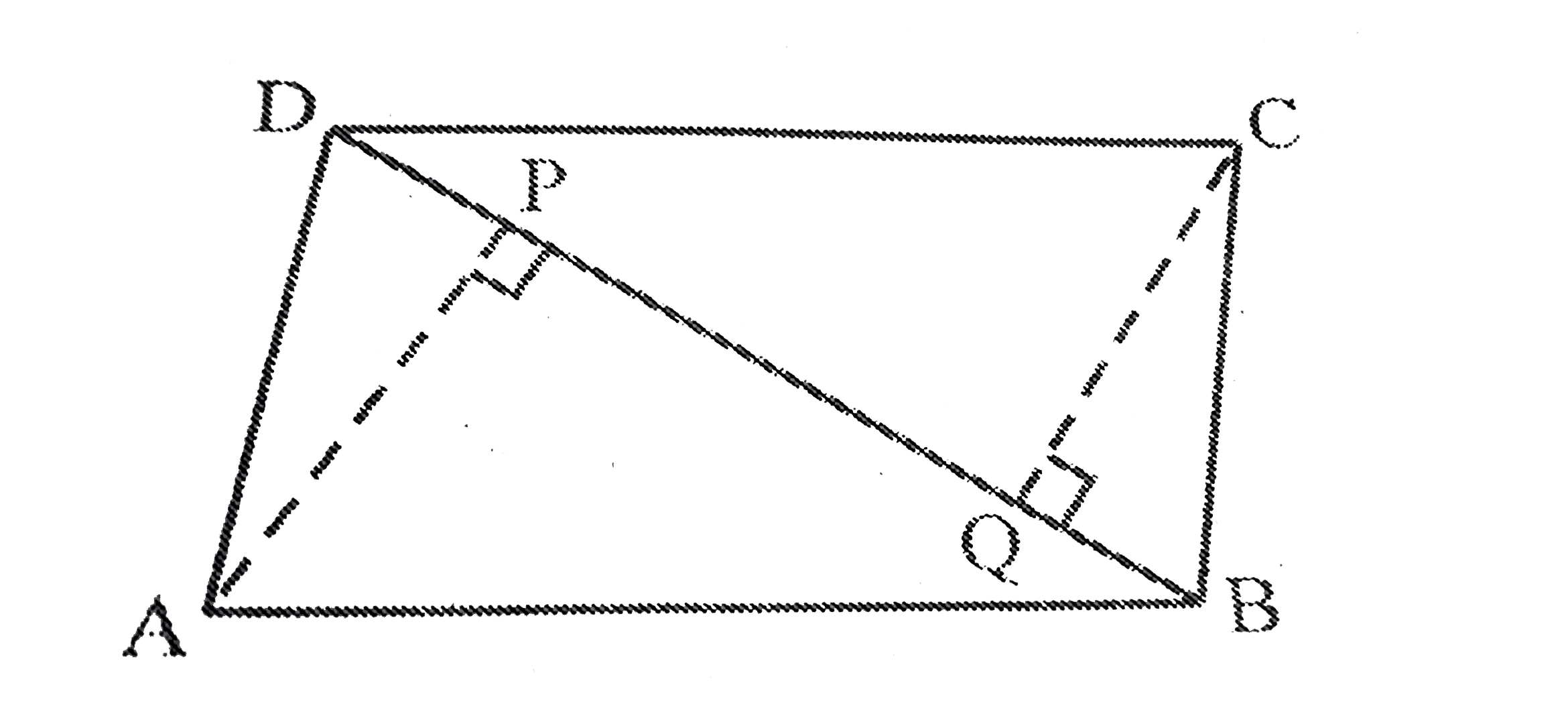
ABCD is a parallelogram and AL and CM are perpendicualrs from vertices A and C on diagonal BD, as shown in the adjoining figure. Show that (i) △ALB≅△CMD and (ii) AL = CM.

In △ALBandCMD, we have
AB=CD (opp. sides of a ||gm)
∠ALB=∠CMD=90∘ [∵AL⊥BD,CM⊥BD]
∠ABL=∠CDM (alt. interior ∠)
∴△ALB≅△CMD (AAS - criterion).
And so, AL=CM (c.p.c.t.).
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
In the adjoining figure a parallelogram ABCD is shown .
AB=24 cm and AO=BO=13 cm. Find BC :
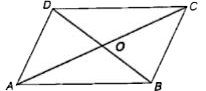 A8 cmB10 cmC11 cmDnone of these
A8 cmB10 cmC11 cmDnone of theseIn the adjoining figure , the ratio of the areas of the parallelogram ABCD and that of triangle ABN is :
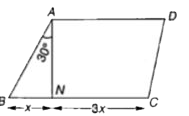 A6:1B5:1C4:1D8:1
A6:1B5:1C4:1D8:1
ABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionDiagonals of a parallelogram ABCD intersect at O.AL and CM are perpendiculars to BD such that L and M lie on BD . IS AL=CM? why or why not?
View SolutionABCD is a quadrilateral and BD is one of its diagonals, as shown in the figure. Prove that quadrilateral ABCD is a parallelogram, also find its area.
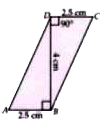
View SolutionIn the adjoining figure, if PA=10 cm, then find the perimeter of ΔPCD.
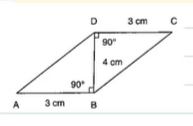
View SolutionABCD is a quadrilateral and BD is one of its diagonals as shown in Figure. Show that ABCD is a parallelogram and find its area.
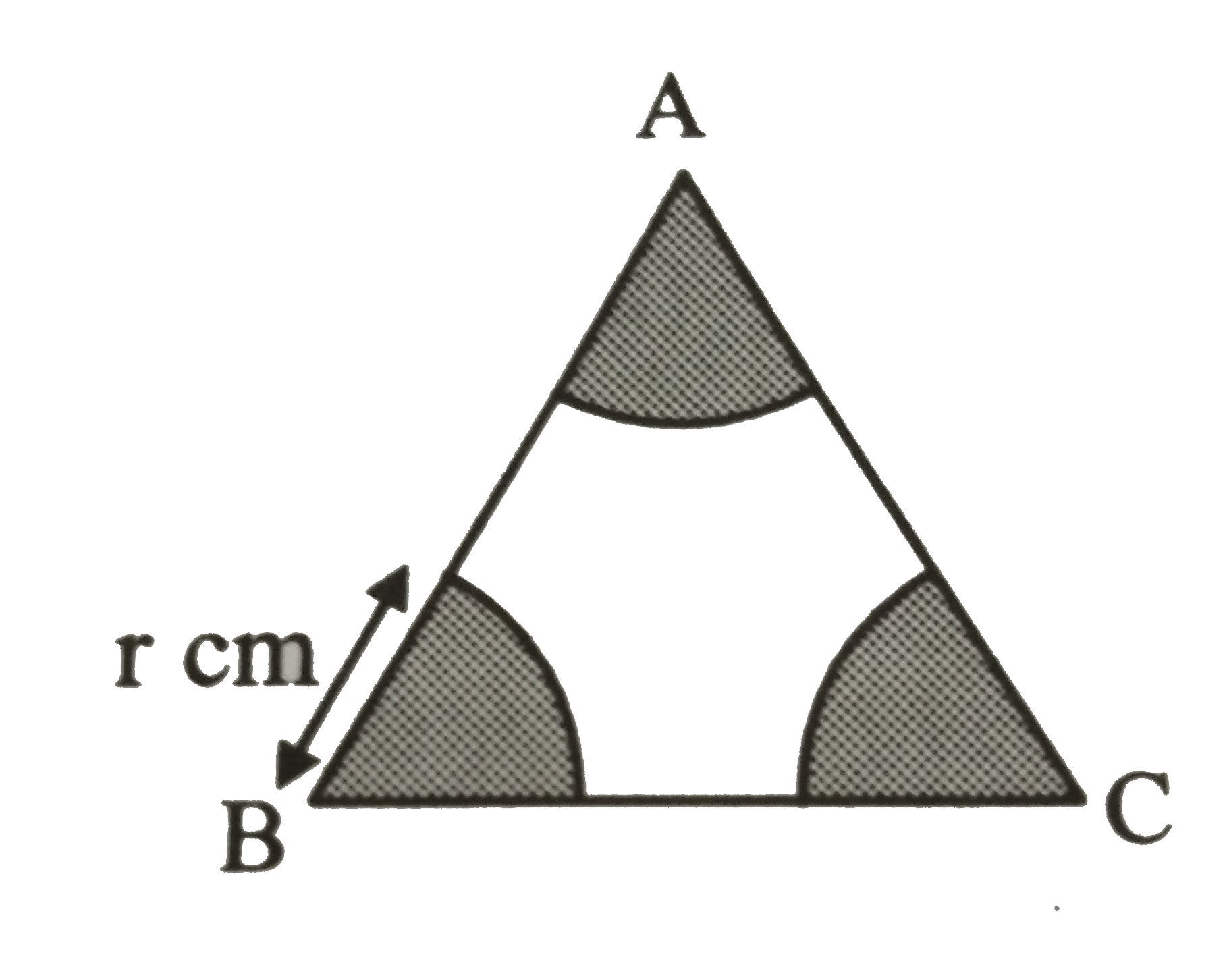
View SolutionIf arcs of radius r cm are drawn with the vertices of an equilateral triangle ABC as shown in the figure, then the area of the shaded region is
View Solution