ABCD is a regular tetrahedron, A is the origin and B lies on x-axis. ABC lies in the xy-plane Under these conditions, the number of possible tetrahedrons is :
The correct Answer is:8
To solve the problem step by step, let's analyze the conditions given for the regular tetrahedron ABCD.
1. Understanding the Tetrahedron:
- A tetrahedron has four vertices. In this case, we have vertices A, B, C, and D.
- A is the origin (0, 0, 0).
- B lies on the x-axis, which means its coordinates can be represented as (x, 0, 0).
2. Finding the Position of B:
- The modulus of the vector AB is given as |AB| = 2. Since A is at the origin, we can say:
|AB|=|B−A|=|B|=2
- Therefore, B can be at (2, 0, 0) or (-2, 0, 0). This gives us 2 possible positions for B.
3. Position of C:
- The triangle ABC lies in the xy-plane. Therefore, the z-coordinate of C must be 0.
- The distance from B to C must also be equal to 2 (since all sides of a regular tetrahedron are equal).
- If B is at (2, 0, 0), C can be at (2, y, 0) or (2, -y, 0) such that:
|BC|=2⇒√(2−2)2+(y−0)2+(0−0)2=2⇒|y|=2
- Thus, C can be at (2, 2, 0) or (2, -2, 0).
- If B is at (-2, 0, 0), similar reasoning applies, and C can be at (-2, 2, 0) or (-2, -2, 0).
- Hence, we have 2 possible positions for C regardless of the position of B.
4. Position of D:
- The vertex D can be positioned above or below the xy-plane. Thus, D can have a z-coordinate of either +z or -z.
- The distance from A to D must also be equal to 2. Therefore, D can be at (0, 0, 2) or (0, 0, -2).
- This gives us 2 possible positions for D.
5. Calculating Total Combinations:
- Now we can combine the possibilities:
- 1 position for A (the origin)
- 2 positions for B
- 2 positions for C
- 2 positions for D
- The total number of possible tetrahedrons is given by:
Total Tetrahedrons=1×2×2×2=8
Thus, the number of possible tetrahedrons is 8.
- A tetrahedron has four vertices. In this case, we have vertices A, B, C, and D.
- A is the origin (0, 0, 0).
- B lies on the x-axis, which means its coordinates can be represented as (x, 0, 0).
- The modulus of the vector AB is given as |AB| = 2. Since A is at the origin, we can say:
|AB|=|B−A|=|B|=2
- Therefore, B can be at (2, 0, 0) or (-2, 0, 0). This gives us 2 possible positions for B.
- The triangle ABC lies in the xy-plane. Therefore, the z-coordinate of C must be 0.
- The distance from B to C must also be equal to 2 (since all sides of a regular tetrahedron are equal).
- If B is at (2, 0, 0), C can be at (2, y, 0) or (2, -y, 0) such that:
|BC|=2⇒√(2−2)2+(y−0)2+(0−0)2=2⇒|y|=2
- Thus, C can be at (2, 2, 0) or (2, -2, 0).
- If B is at (-2, 0, 0), similar reasoning applies, and C can be at (-2, 2, 0) or (-2, -2, 0).
- Hence, we have 2 possible positions for C regardless of the position of B.
- The vertex D can be positioned above or below the xy-plane. Thus, D can have a z-coordinate of either +z or -z.
- The distance from A to D must also be equal to 2. Therefore, D can be at (0, 0, 2) or (0, 0, -2).
- This gives us 2 possible positions for D.
- Now we can combine the possibilities:
- 1 position for A (the origin)
- 2 positions for B
- 2 positions for C
- 2 positions for D
- The total number of possible tetrahedrons is given by:
Total Tetrahedrons=1×2×2×2=8
Topper's Solved these Questions
Similar Questions
ABCD is a regular tetrahedron P & Q are the mid -points of the edges AC and AB respectively, G is the cenroid of the face BCD and θ is the angle between the vectors −−→PG and −−→DQ, then
View SolutionABCD is square in which A lies on positive y-axis and B lies on the positive x-axis. If D is the point (12, 17), then co-ordinate of C is
View SolutionIf O be the origin and OP=r and OP makes an angle θ with the positive direction of x-axis and lies in the XY plane find the coordinates of P.
View SolutionComprehesion-I
Let k be the length of any edge of a regular tetrahedron (all edges are equal in length). The angle between a line and a plane is equal to the complement of the angle between the line and the normal to the plane whereas the angle between two plane is equal to the angle between the normals. Let O be the origin and A,B and C vertices with position vectors →a,→b and →c respectively of the regular tetrahedron.
The value of [→a→b→c]2 is
View SolutionComprehesion-I
Let k be the length of any edge of a regular tetrahedron (all edges are equal in length). The angle between a line and a plane is equal to the complement of the angle between the line and the normal to the plane whereas the angle between two plane is equal to the angle between the normals. Let O be the origin and A,B and C vertices with position vectors →a,→b and →c respectively of the regular tetrahedron.
The angle between any edge and a face not containing the edge is
View SolutionComprehesion-I
Let k be the length of any edge of a regular tetrahedron (all edges are equal in length). The angle between a line and a plane is equal to the complement of the angle between the line and the normal to the plane whereas the angle between two plane is equal to the angle between the normals. Let O be the origin and A,B and C vertices with position vectors →a,→b and →c respectively of the regular tetrahedron.
The angle between any two faces is
View SolutionA triangle has two of its vertices at (0,1) and (2,2) in the cartesian plane. Its third vertex lies on the x-axis. If the area of the triangle is 2 square units then the sum of the possible abscissae of the third vertex, is-
View SolutionA circular hole of radius R/2 is cut from a circular disc of radius R. The disc lies in the xy-plane and its centre coincides with the origin. If the remaining mass of the disc is M, then
a. determine the initial mass of the disc and
b. determine its moment of inertia about the z-axis.
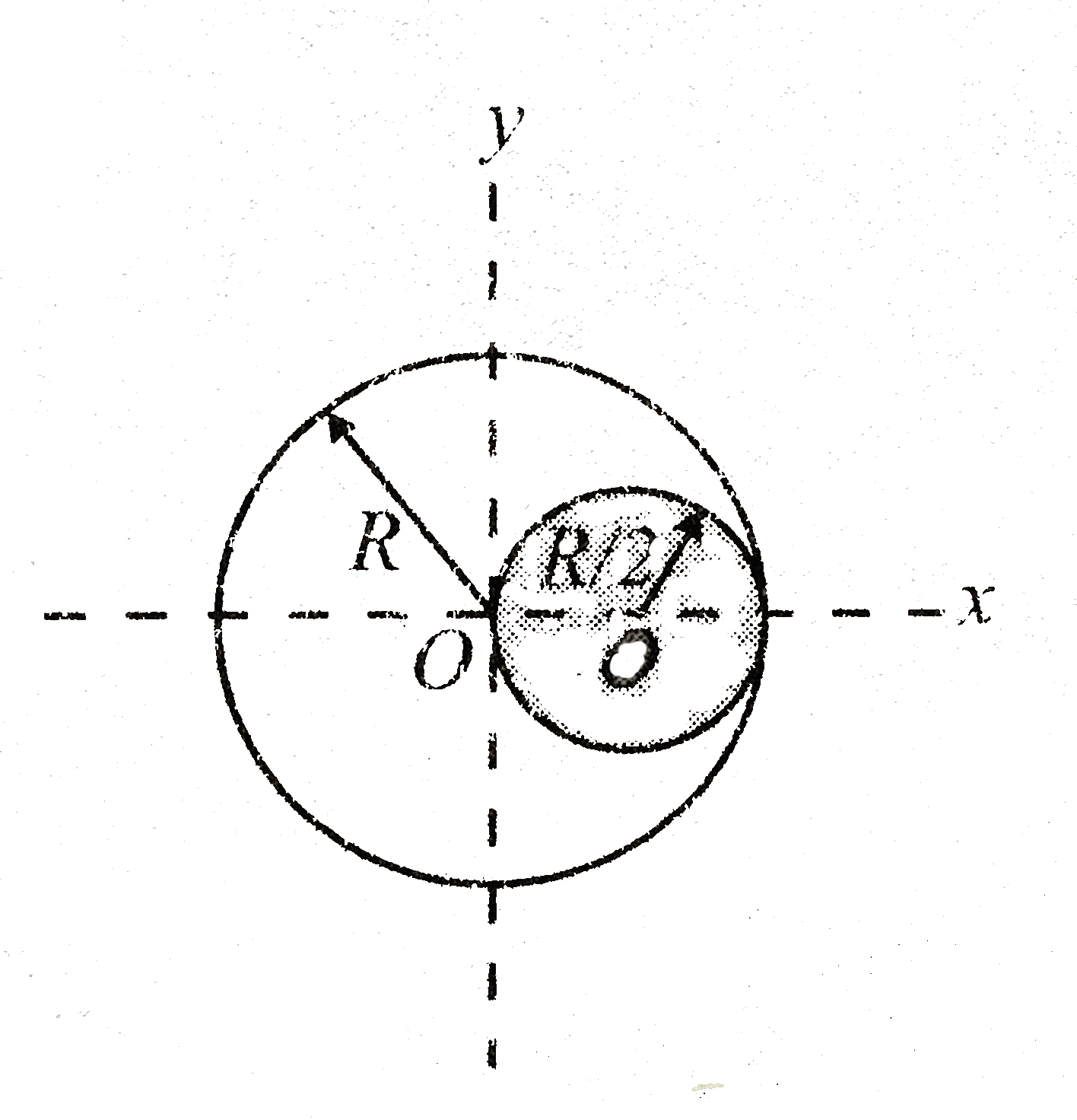
View SolutionA circle is drawn whose centre is on the x - axis and it touches the y - axis. If no part of the circle lies outside the parabola y2=8x, then the maximum possible radius of the circle is
View SolutionOABCDE is a regular hexagon of side 2 units in the XY-plane in the first quadrant. O being the origin and OA taken along the x-axis. A point P is taken on a line parallel to the z-axis through the centre of the hexagon at a distance of 3 unit from O in the positive Z direction. Then find vector AP.
View Solution
