ABCD is a trapezium in which ABIIDC and P and Qare points on AD and BC respectively such that PQ||DC. If PD= 12 cm, BQ = 42 cm and QC = 18cm, find AD.
The correct Answer is:AD=40cm
To solve the problem step by step, we will use the properties of trapeziums and the Basic Proportionality Theorem.
Step 1: Understand the trapezium and the given points
We have a trapezium ABCD where AB is parallel to DC. Points P and Q are on sides AD and BC respectively, and line segment PQ is parallel to DC.
Step 2: Identify the lengths given in the problem
- PD = 12 cm
- BQ = 42 cm
- QC = 18 cm
Step 3: Use the Basic Proportionality Theorem
According to the Basic Proportionality Theorem (also known as Thales' theorem), if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
In triangle BDC:
OBOD=BQQC
Let OB=x and OD=y. Then we have:
xy=4218
Simplifying this gives:
xy=73
This means 3x=7y or x=73y (Equation 1).
Step 4: Apply the theorem in triangle ADB
In triangle ADB, since OP is parallel to AB:
ODOB=PDAP
Using PD=12 cm, we can write:
yx=12AP
Rearranging gives:
AP=12xy(Equation2)
Step 5: Substitute Equation 1 into Equation 2
From Equation 1, we know x=73y. Substitute this into Equation 2:
AP=12⋅73yy
This simplifies to:
AP=12⋅73=28 cm
Step 6: Find the length of AD
Now, we can find the length of AD:
AD=AP+PD
Substituting the values we found:
AD=28 cm+12 cm=40 cm
Final Answer
Thus, the length of AD is 40 cm.
---
We have a trapezium ABCD where AB is parallel to DC. Points P and Q are on sides AD and BC respectively, and line segment PQ is parallel to DC.
- PD = 12 cm
- BQ = 42 cm
- QC = 18 cm
According to the Basic Proportionality Theorem (also known as Thales' theorem), if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
OBOD=BQQC
Let OB=x and OD=y. Then we have:
xy=4218
Simplifying this gives:
xy=73
This means 3x=7y or x=73y (Equation 1).
In triangle ADB, since OP is parallel to AB:
ODOB=PDAP
Using PD=12 cm, we can write:
yx=12AP
Rearranging gives:
AP=12xy(Equation2)
From Equation 1, we know x=73y. Substitute this into Equation 2:
AP=12⋅73yy
This simplifies to:
AP=12⋅73=28 cm
Now, we can find the length of AD:
AD=AP+PD
Substituting the values we found:
AD=28 cm+12 cm=40 cm
Thus, the length of AD is 40 cm.
Topper's Solved these Questions
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - PROFICIENCY EXERCISE (LONG ANSWER QUESTIONS)
15 Videos
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SELF ASSESSMENT TEST
10 Videos
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - PROFICIENCY EXERCISE (VERY SHORT ANSWER QUESTIONS)
14 Videos
- REAL NUMBERSBOOK - VK GLOBAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self -Assessment Test
11 Videos
- VALUE-BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-VII : (Statistics & Probability)
8 Videos
Similar Questions
ABCD is a trapezium in which AB || DCand P, Qare points on AD and BC respectively, such that PQ II DC. If PD - 18 cm, BQ = 35 cm and QC = 15 cm, then find the length of AD.
View SolutionABCD is a trapezium in which AB||DC and P,Q are points on AD and BC respectively, such that PQ||DC, if PD=18 cm, BQ=35 cm and QC=15 cm. Find AD.
View Solution
Knowledge Check
ABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
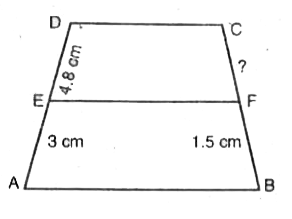 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of theseABCD is a trapezium of sides in which BC || AB & AB=9cm, BC=12cm, CD=15cm & DA=20cm. Find the sum of square of its diagonal.
A638B786C838D814ABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
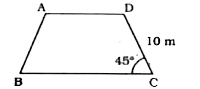 A10√2mB4√2mC5√2mD6√2m
A10√2mB4√2mC5√2mD6√2m
If D and E are points on the sides AB and AC respectively of DetlaABC such that AB=5.6cm,AD=1.4cm,AC=7.2cmandAE=1.8cm. Show that DE∣∣BC.
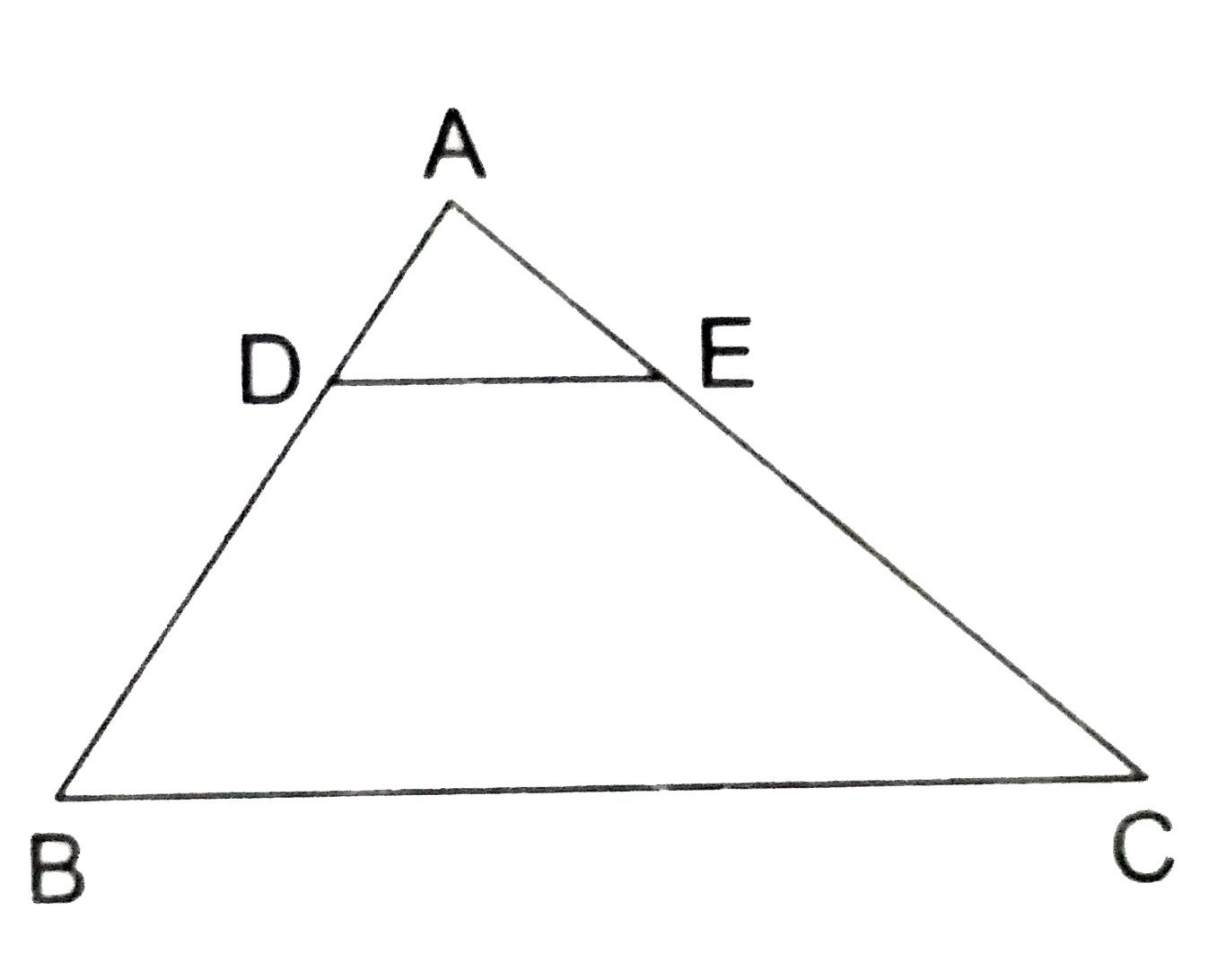
View SolutionIn a trapezium ABCD, P and Q are points on AD and Bc respectively such that DPAP=CQBQ=13.If the diagonal BD intersects PQ at E,find the ratio of arΔDPE toarea of trapezium ABCD.
View SolutionABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View SolutionIn ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
View SolutionABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=
View Solution
