An arc of a circle is a length 5πcm and the sector it bounds has an area of 20πcm2 . Find the radius of the circle.
To find the radius of the circle given the length of the arc and the area of the sector, we can follow these steps:
1. Identify the Given Values:
- Length of the arc L=5πm
- Area of the sector A=20πm2
2. Use the Formula for Length of Arc:
The formula for the length of an arc is given by:
L=πrθ180
where r is the radius and θ is the angle in degrees.
3. Use the Formula for Area of Sector:
The formula for the area of a sector is given by:
A=πr2θ360
4. Express θ from the Length of Arc Formula:
Rearranging the length of arc formula to find θ:
θ=180Lπr
5. Substitute θ into the Area of Sector Formula:
Now substitute θ into the area of the sector formula:
A=πr2360⋅180Lπr
Simplifying this gives:
A=180Lr360=Lr2
6. Substitute the Known Values:
Now substitute the values of A and L:
20π=(5π)r2
7. Solve for r:
To isolate r, multiply both sides by 2:
40π=5πr
Now divide both sides by 5π:
r=40π5π=8m
8. Conclusion:
The radius of the circle is r=8m.
- Length of the arc L=5πm
- Area of the sector A=20πm2
The formula for the length of an arc is given by:
L=πrθ180
where r is the radius and θ is the angle in degrees.
The formula for the area of a sector is given by:
A=πr2θ360
Rearranging the length of arc formula to find θ:
θ=180Lπr
Now substitute θ into the area of the sector formula:
A=πr2360⋅180Lπr
Simplifying this gives:
A=180Lr360=Lr2
Now substitute the values of A and L:
20π=(5π)r2
To isolate r, multiply both sides by 2:
40π=5πr
Now divide both sides by 5π:
r=40π5π=8m
The radius of the circle is r=8m.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a sector of a circle has an arc length of 2π inches and an area of 6π square inches, what is the length of the radius of the circle?
A1B2C3D6Circle O (not shown) is divided into three sectores. Point P, Q and R are on the circumference of the circle. Sector POR has an area of 8π, and sector ROQ has an area of 6π. IF the radius of circle O is 4, what is the measure of the central angle of sector QOP, in degrees?
A45B90C135D180
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2 , then the radius of the circle is
(a) 12 cm
(b) 16 cm
(c) 8 cm
(d) 10 cm
View SolutionAn arc of length 20π cm subtends an angle of 144o at the centre of a circle. Find the radius of the circle.
View SolutionA sector of 56∘ cut out from a circle contains area 4.4cm2. Find the radius of the circle
View SolutionA circle is drawn in a sector of a larger circle of radius r, as shown in the adjacent figure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the small circle is-

View SolutionA circle is drawn in a sectore of a larger circle of radius r, as shown in fugure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the smaller circle is
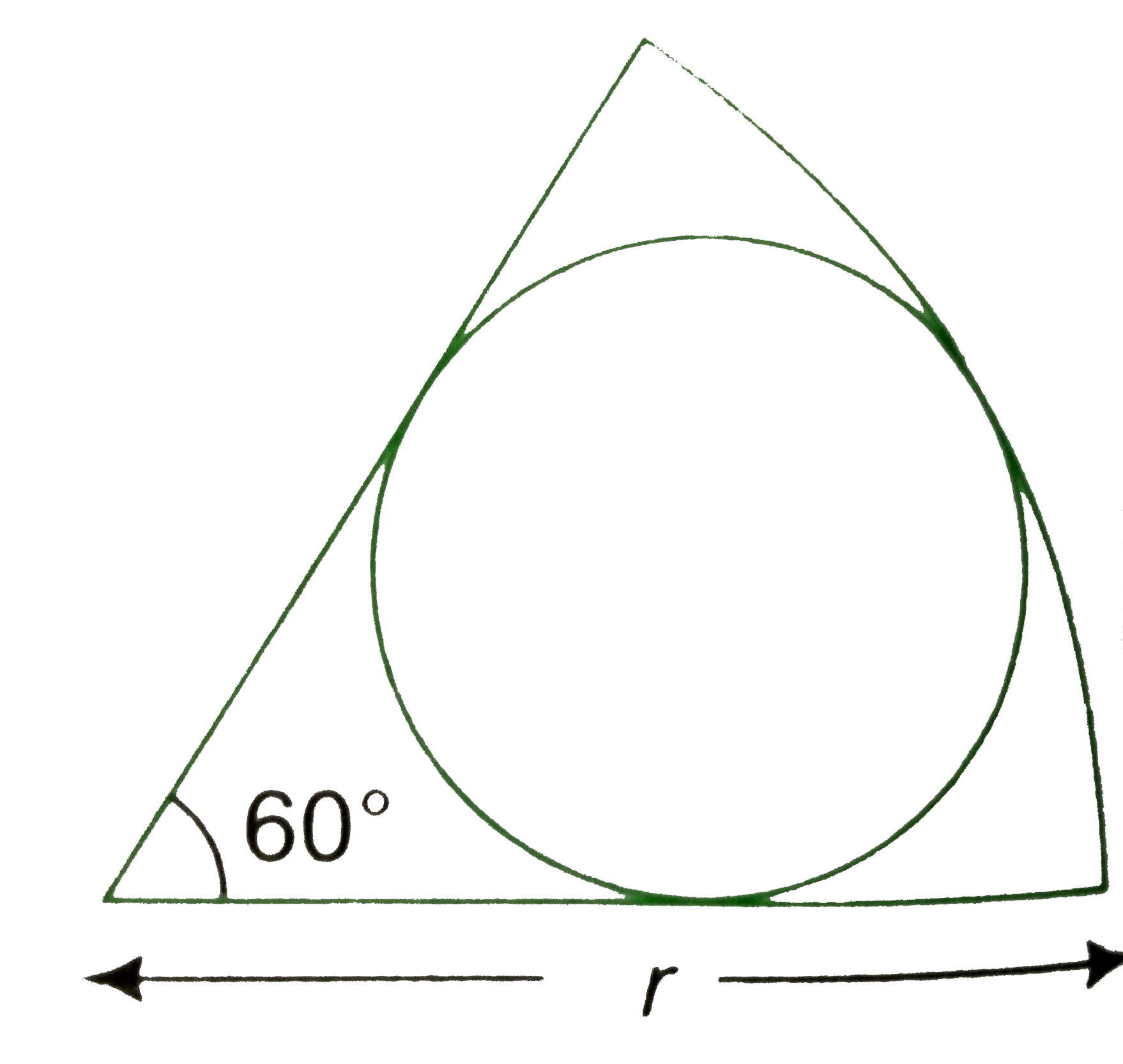
View SolutionAn arc of length 15 cm subtends an angle of 45∘ at the center of a circle. Find in terms of π , the radius of the circle.
View Solution
