An oil tank has the shape of a right circular cylinder is 12 centimeters in height and has a volume of 108π cubic centimeters. What is the diameter of the base of the cylinder, in centimeters?
The correct Answer is:6
To find the diameter of the base of the cylinder, we can follow these steps:
Step 1: Write down the formula for the volume of a cylinder.
The volume V of a right circular cylinder is given by the formula:
V=πr2h
where r is the radius and h is the height.
Step 2: Substitute the known values into the formula.
We know the volume V=108π cubic centimeters and the height h=12 centimeters. Substituting these values into the formula gives:
108π=πr2⋅12
Step 3: Simplify the equation.
We can cancel π from both sides of the equation:
108=r2⋅12
Step 4: Solve for r2.
Next, we divide both sides by 12 to isolate r2:
r2=10812
Calculating the right side gives:
r2=9
Step 5: Solve for r.
Now, we take the square root of both sides to find r:
r=√9=3
Step 6: Calculate the diameter.
The diameter d of the cylinder is twice the radius:
d=2r=2×3=6
Final Answer:
The diameter of the base of the cylinder is 6 centimeters.
---
The volume V of a right circular cylinder is given by the formula:
V=πr2h
where r is the radius and h is the height.
We know the volume V=108π cubic centimeters and the height h=12 centimeters. Substituting these values into the formula gives:
108π=πr2⋅12
We can cancel π from both sides of the equation:
108=r2⋅12
Next, we divide both sides by 12 to isolate r2:
r2=10812
Calculating the right side gives:
r2=9
Now, we take the square root of both sides to find r:
r=√9=3
The diameter d of the cylinder is twice the radius:
d=2r=2×3=6
The diameter of the base of the cylinder is 6 centimeters.
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Multiple Choice
99 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
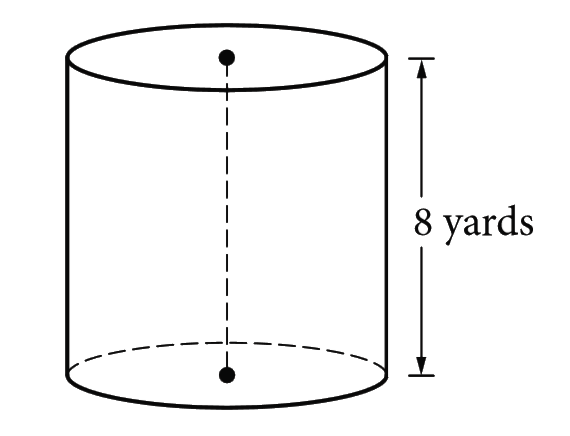
A dairy farmer uses a storage silo that is in the shape of the right circular cylinder above. If the volume of the silo is 72π cubic yards, what is the diameter–––––––––– of the base of the cylinder, in yards?
View SolutionThe diameter of the base of a right circular cylinder is 42cm and its height is 10cm. Find the volume of the cylinder.
View Solution
Knowledge Check
A right circular cone has a volume of 24π cubic inches. If the height of the cone is 2 inches, what is the radius, in inches, of the base of the cone?
A2√3B6C12D36
The area of the base of a right circular cylinder is 42πcm2 and height is 3.5 cm. Find its volume.
View SolutionThe area of the base of a right circular cylinder is 616cm2 and its height is 25cm. Find the volume of the cylinder.
View SolutionThe area of the base of a right circular cylinder is 154 cm2 and its height is 15cm. Find the volume of the cylinder.
View SolutionThe area of the base of a right circular cylinder is 154 cm2 and its height is 15cm. Find the volume of the cylinder.
View SolutionThe volume of right circular cylinder A is 22 cubic centimeters. What is the volume , in cubic centimetres, of a right circular cylinder with twice the radius and half the height of cylinder A?
View SolutionThe height and radius of the base of a right circular cylinder is 'r'. Find its totalsurface area.
View SolutionA cylinder has a surface area of 360π and height of 3. What is the diameter of the cylinder's circular base?
View Solution
