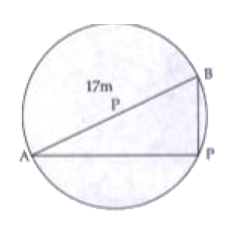
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find a quadratic equations in variable x for above situation.
x2+7x−120=0
x2+5x−120=0
x2+7x−120=0
None of these
The correct Answer is:A
Step by step video & image solution for Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m. Find a quadratic equations in variable x for above situation. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRATIC EQUATIONSBOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Multiple Choice Question
59 Videos
- QUADRATIC EQUATIONSBOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Very Short Answer Type Question
33 Videos
- QUADRATIC EQUATIONSBOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Assertion and Reason Based MCQs
8 Videos
- PROBABILITYBOOK - OSWAL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Self Assessment
66 Videos
- REAL NUMBERSBOOK - OSWAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self-Assessment
11 Videos
Similar Questions

Aniket is studying in X standard. He created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the area of triangle ABP.
View Solution
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the distance between pole and gate B.
View Solution
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
Find the distance between pole and gate A.
View Solution
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gets A and B on the boundary is 7m.
What is the length of (AP+BP) ?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionA thin insulating wire is stretched·along the diameter of an. insulated circular hoop of radius R. A small bead of mass m and charge-q is threaded onto the wire. Two small identical charges are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread as shown in figure. The bead is released at a point which.is located at a distance x0 from the centre of the hoop. Assume that x0<<R.
(a) What is the resultant force acting on the charged bead?
(b) Describe the motion of the bead after it is released X
(c) Use the assumption that xR<<1 to obtain an approximate equation of motion, and find the displacement and velocity of the bead as functions of time
(d) When will the velocity of the bead will bcome zero for the first time?

View SolutionA thin insulating wire is stretched along the diameter of an insulated circular hoop of radius E. A small bead of mass m and charge –q is threaded onto the wire. Two small identical charge= are tied to the hoop at points opposite to each other, so that the diameter passing throughtheL-is perpendicular to the thread (see figure). The bead is released at a point which is a distance-, from the centre of the hoop. Assume that x0<<R.
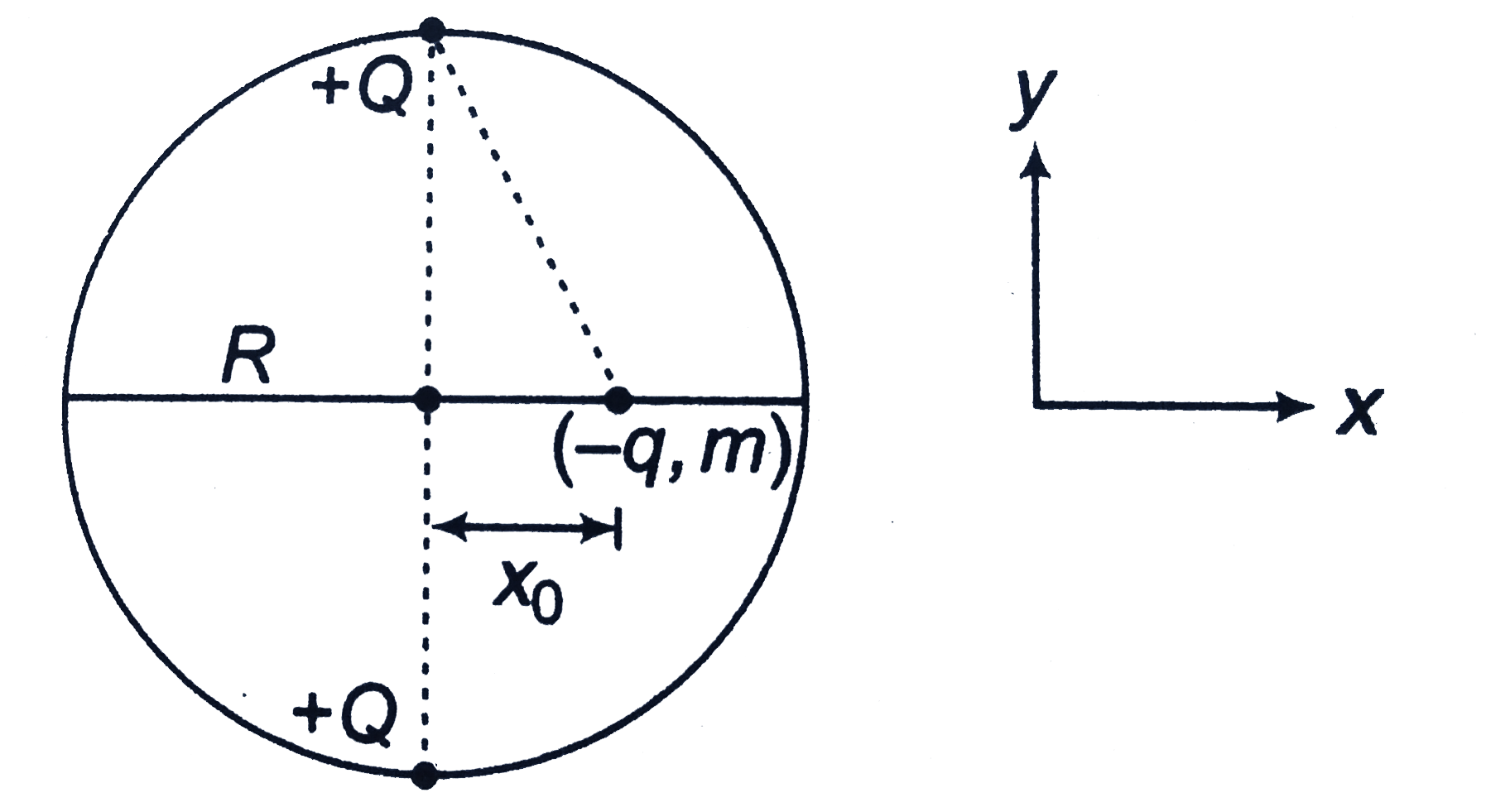
a. What is the resultant acting on the charged bead?
b. Describe (qualitatively) the motion of the bead after it is released.
c. Use the assumption that x/R<<1 to obtain an approximate equation of motinand find the dislacemet ad velocity of the bead as functuions of time.
d. When will the velocity of the bead will become zero for the first time?
View SolutionA uniform rod of length L is rotating in a horizontal plane about a vertical axis passing through one of its ends. At a distance x(<L) from the axis there is a fixed vertical pole. The rod hits the pole and its direction of motion is reversed. Find x if it is known that during the impact the axis of rotation imparts no impulse to the rod. Does your answer depend on coefficient of restitution?
[NOTE : If you hit a lamp post with a rod, the hand holding the rod gets hurt as long as the impact misses the so called sweet spot of the rod (and hits either above or below the sweet spot). After solving the above problem you know where the sweet spot is ! You may assume that during the impact the rod is rotating about its holding hand. And if you play cricket, you know that there is a sweet spot in your bat too ! If the ball hits way above or below the spot you get stung.]
View SolutionA 3m long arm OA rotates in a plane such that 0 = 0.5 t2 where is the angle with x-axis in radian and t is in second. A slider collar B slides along the arm in such a way that its distance from the hinge O is given by r = 3 - 0.412 where r is in meters. Find the speed of the collar at t = 18:- A B В
View Solution
