Answer the following by a number or a word or a sentence :
In △ABC , AD ia a median. If AB= 6 cm, AC= 8 cm and AD= 5 cm, find BC.Solution in Gujrati
The correct Answer is:10cm
Step by step video, text & image solution for Answer the following by a number or a word or a sentence : In triangleABC , AD ia a median. If AB= 6 cm, AC= 8 cm and AD= 5 cm, find BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In ΔABC, D and E are points on the sides AB and AC respectively such that DE∣∣BC. If AB=6.75cm,AC=8.50cm and EC=6.80cm. Then find BD.
View SolutionThe slant height of a frustum of a cone is 4 m and the perimeter of circular ends are 18 m and 16 m. Find the cost of painting its curved surface at 10 per sq. m.
View Solutionएक ΔABC बनाया जिसमे AB=6 सेमी , BC = 6 सेमी तथा माधियका AD = 4 सेमी है ।
View SolutionIn ΔABC, AD is the bisector of ∠BAC. If AB=8cm, BD=6cm and DC=3cm, then find AC.
View SolutionΔABC में, ∠A का समद्विभाजक AD है, तो CD ज्ञात करें, यदि
AB= 6 सेमी ., AC = 5 सेमी ., BD = 3 सेमी
View SolutionΔABC में, ∠A का समद्विभाजक AD है, तो BC ज्ञात करें, यदि
AB= 5.6 सेमी., AC = 4 सेमी., DC = 3 सेमी
View SolutionΔABC में, ∠A का समद्विभाजक AD है, तो BC ज्ञात करें, यदि
AB = 5 सेमी., AC= 4 सेमी., BD = 2.5 सेमी
View SolutionΔABC में, ∠A का समद्विभाजक AD है, तो BC ज्ञात करें, यदि
AB = 5.6 सेमी., AC = 6 सेमी., DC = 3 सेमी.
View Solutionचित्र में, ΔABC की माध्यिका AD=6 सेमी है । यदि आधार BC = 8 सेमी हो, तो AB2+AC2 का मान है
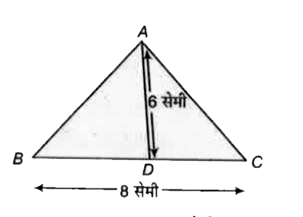
View SolutionIn the triangle ABC, AB = 5 cm, AC = 6 cm and BC = 8 cm, what will be the length of the median AD?
View SolutionConstruct a triangle ABC such that BC=6 cm AB =6 cm and median AD=5 cm
View SolutionIn a ΔABC,AB=5cm,AC=7cm,BC=6cm, If AD⊥BC BC. Find the length of BD.
View SolutionIn a ΔABC,AB=5,AC=6cm,BC=8cm . Find the length of median AD.
View SolutionConstruct a triangle ABC in which AB = 5 cm, BC = 6-8 cm and median AD = 4.4 cm. Draw incircle of this triangle.
View SolutionIn △ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is:
View Solution
