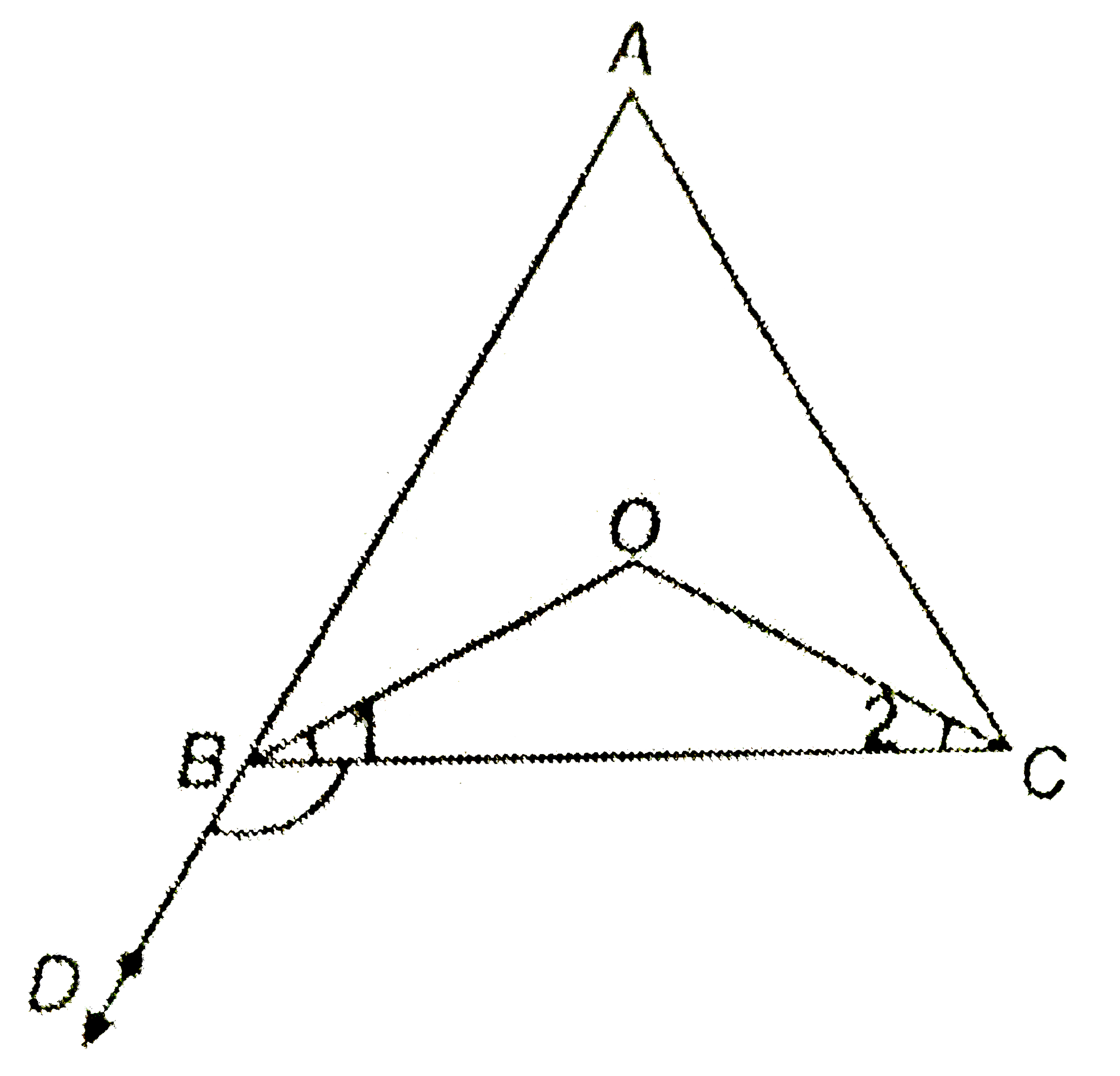
Bisectors of the angles B and C of an isosceles ΔABC with AB=AC intersect each other at O. Show that external angle adajcent to ∠ABC is equal to ∠BOC.
In ΔABC, we have AB=AC
∴∠B=∠C (∵ angles opposite to equal sides of a triangle are equal)
∴12∠B=12∠C ...(1)
In ΔOBC, we have
∠1=12∠B and ∠2=12∠C
∴∠1=∠2 [from (1)]
∠DBC+∠1+∠OBA=180∘ [∵ABD is a straight line]
⇒ ∠DBC+2∠1=180∘ [∵∠1=∠OBA] ...(2)
In ΔOBC,
∠1+∠2+an≥BOC=180∘ [∴∠1=∠2] ...(3)
From (2) and (3), we get
∠DBC+2∠1+∠BOC
⇒ ∠DBC=∠BOC
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
The bisectors of ∠Band∠C of an isosceles triangle with AB=AC intersect each other at a point O.BO is produced to meet AC at a point M. Prove that ∠MOC=∠ABC.
View SolutionThe bisectors of angles A and B of a scalene triangle ABC meet at O.
What is the point O called ?
View SolutionABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View SolutionConstruct an isosceles ΔABC such that AB=AC=5cmand∠A=60∘.
View SolutionIn triangle LMN, bisector of interior angles at L and N intersect each other at point A. Prove that :
AM bisects angle LMN.
View SolutionThe bisectors of angles A and B of a scalene triangle ABC meet at O.
What is the relation between angle ACO and angle BCO?
View SolutionDetermine the measure of each of the equal angles of a right-angled isosceles triangle.
View SolutionConstruct an isosceles ΔABC such that AB=BC=5.4cmand∠B=30∘.
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A.
View Solution
