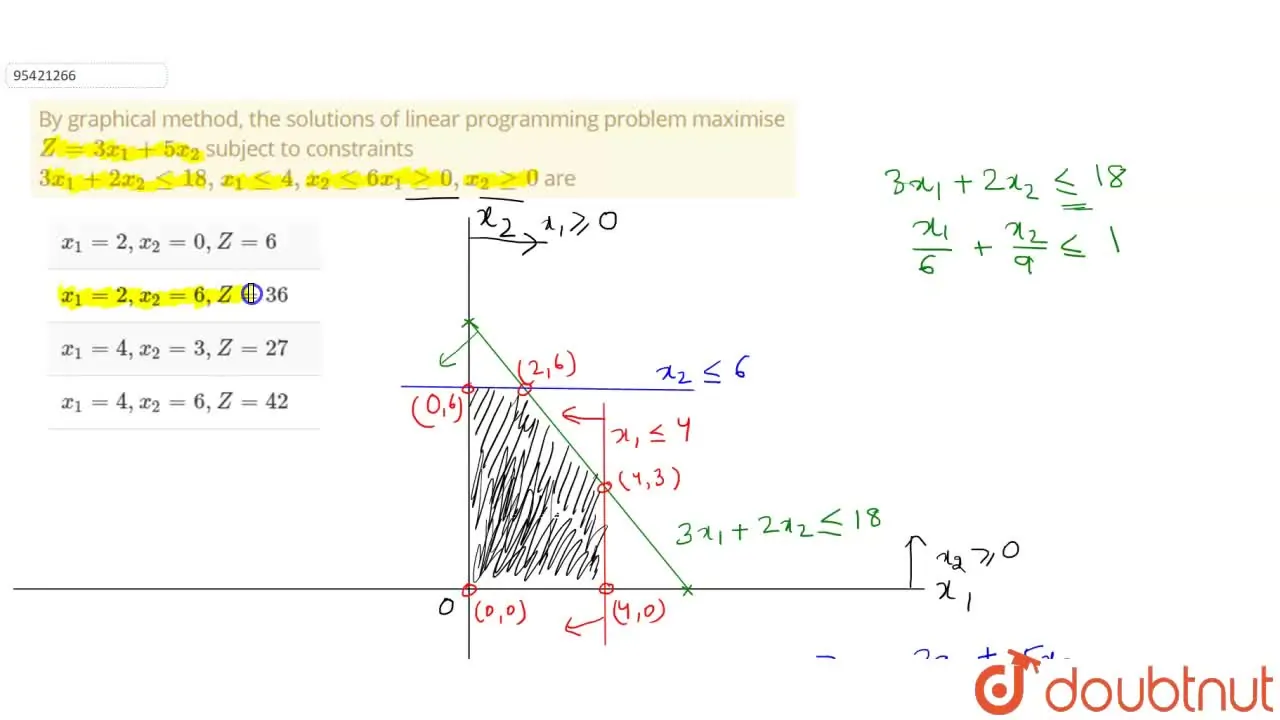
By graphical method, the solutions of linear programming problem maximise Z=3x1+5x2 subject to constraints 3x1+2x2≤18,x1≤4,x2≤6x1≥0,x2≥0 are
x1=2,x2=0,Z=6
x1=2,x2=6,Z=36
x1=4,x2=3,Z=27
x1=4,x2=6,Z=42
The correct Answer is:B
Step by step video, text & image solution for By graphical method, the solutions of linear programming problem maximise Z=3x_(1)+5x_(2) subject to constraints 3x_(1)+2x_(2) le 18, x_(1) le 4, x_(2) le 6 x_(1) ge0,x_(2) ge 0 are by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
By graphical method, the solutions of linear programming problem maximum Z=3x1+5x2 subject to constraints 3x1+2x2≤18
x1≤4,x2≤6,x1≥0,x2≥0View SolutionThe linear programming problem Maximise Z=x1+x2
Subject to constraints
x1+2x2≤2000x1+x2≤1500x2≤600x1≥0 hasView SolutionThe linear programming problem : Maximize z=z=x1+x2 subject to constraints x1+2x2≤2000,x1+x2≤1500,x2≤600,x1≥0 has
View SolutionThe iinear programming problem Maximise Z=x1+x2
Subject to constraints
x1+2x2≤≤2000
x1+x2≤15000
x2≤600
x1≥hasView SolutionFor L.P.P. maximize z=4x1+2X2 subject to 3x1+2x2≥9,x1−x2≤3,x1≥0,x2≥0 has ……
View SolutionMaximize z=x1+3x2
Subject to
3x1+6x2≤8
5x1+2x2≤10
and x1,x2≥0View SolutionMaximize z=5x1+3x2
Subject to
3x1+5x2≤15
5x1+2x2≤10
x1,x2≥0View SolutionMaximize z=−x1+2x2
Subject to
−x1+x2≤1
−x1+2x2≤4
x1,x2≤0View SolutionThe linear programming problem minimiseZ=3x+2y subject to the constraints
x+y≥8
3x+5y≤15
x≥0,y≥0 hasView SolutionSolve the linear programming problem. Maximise Z = x + 2y
Subject to constraints x−y≤10,2x+3y≤20 and x≥0,y≥0View Solution