Consider two straight lines, each of which is tangent to both the circle $x^{2} + y^{2} = \frac{1}{2}$ and the parabola $y^{2} = 4 x$ . Let these lines intersect at the point $Q$ . Consider the ellipse whose center is at the origin $O (0, 0)$ and whose semi-major axis is $O Q$ . If the length of the minor axis of this ellipse is $\sqrt{2}$ , then which of the following statement(s) is (are) TRUE? For the ellipse, the eccentricity is $\frac{1}{\sqrt{2}}$ and the length of the latus rectum is 1 (b) For the ellipse, the eccentricity is $\frac{1}{2}$ and the length of the latus rectum is $\frac{1}{2}$ (c) The area of the region bounded by the ellipse between the lines $x = \frac{1}{\sqrt{2}}$ and $x = 1$ is $\frac{1}{4 \sqrt{2}} (π - 2)$ (d) The area of the region bounded by the ellipse between the lines $x = \frac{1}{\sqrt{2}}$ and $x = 1$ is $\frac{1}{16} (π - 2)$ Solution in Tamil

For the ellipse, the eccentricity is $\frac{1}{\sqrt{2}}$ and the length the latcus rectue is 1

For the ellipse, the eccentricity is $\frac{1}{2}$ and the length the latcus rectue is $\frac{1}{2}$

The erea of the reagion bounded by the ellipse between the lines $x = \frac{1}{\sqrt{2}} and x = 1 is \frac{1}{4 \sqrt{4}} (π - 2)$

The erea of the region bounded by the ellipse between the lines $x = \frac{1}{\sqrt{2}} and x = 1 is \frac{1}{16} (π - 12)$

Video Solution

Text Solution

Verified by Experts

Equation of tangent of parabola $y^{2} = 4 x$ having slop is $y = m x + \frac{1}{m}$ ltbr If this is tangent to circle $x^{2} + y^{2} = 1 / 2$ .
If this is tangent of circle $x^{2} + y^{2} = 1 / 2$ , then distance form centre of the circle from the line is equal to radius.
$∴ ∣ ∣ ∣ ∣ \frac{0 + 0 + \frac{1}{m}}{\sqrt{1 + m^{2}}} ∣ ∣ ∣ ∣ = \frac{1}{\sqrt{2}}$
$∴ m^{4} + m^{2} - 2 = 0$
$∴ m = \pm$
Euqation of common tangens are $y = x + 1 and y = - x - 1$
These tangents intersects at point Q which is (-1,0) .
$∴ O Q = 1$
Let the equation of ellipese be $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
$∴ a = O Q = 1$
Let the equation of ellipse be $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
$∴ a = O Q = 1$
also, given that $2 b = \sqrt{2} or b = \frac{1}{\sqrt{2}}$
Thererfore, equation of ellipse is $\frac{x^{2}}{1} + \frac{y^{2}}{1 / 2} = 1$
$e = \sqrt{1 - \frac{b^{2}}{a^{2}}} = \sqrt{1 - \frac{1}{2}} = \frac{1}{\sqrt{2}}$
$L . R . = \frac{2 b^{2}}{a} = 1$

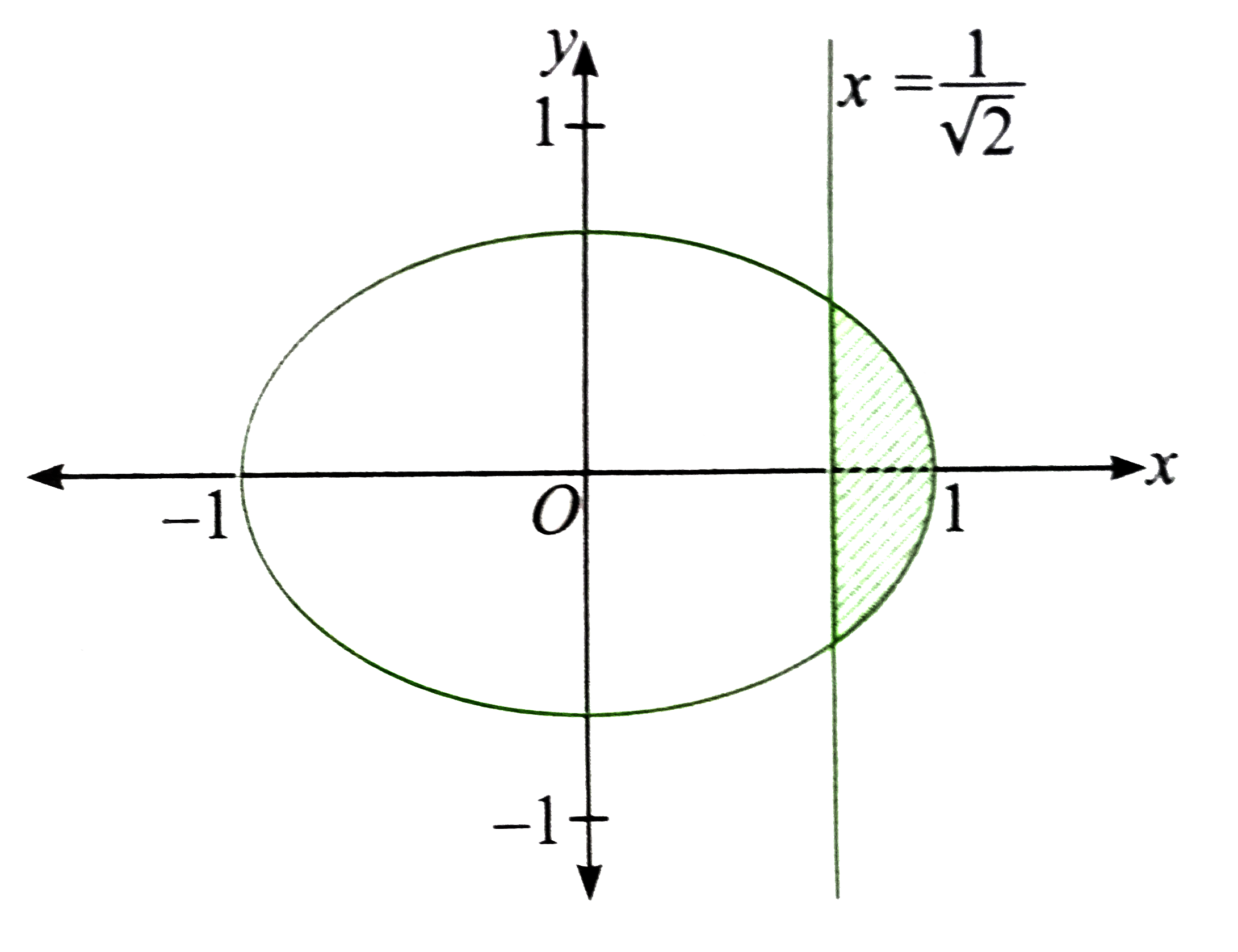
Leh the area bounded by ellipse and lines $x = \frac{1}{\sqrt{2}} and x = 1$ be A.
$A = 2 \times 1 \int 1 / \sqrt{2} \frac{1}{\sqrt{2}} \sqrt{1 - x^{2}} d x$
$= \sqrt{2} {[\frac{x}{2} \sqrt{1 - x^{2}} + \frac{1}{2} {sin}^{- 1} x]}_{1 / \sqrt{2}}^{1}$
$= \sqrt{2} [\frac{π}{4} - (\frac{1}{4} + \frac{π}{8})] = \sqrt{2} (\frac{π}{8} - \frac{1}{4}) = \frac{π - 2}{4 \sqrt{2}}$

Updated on:21/07/2023