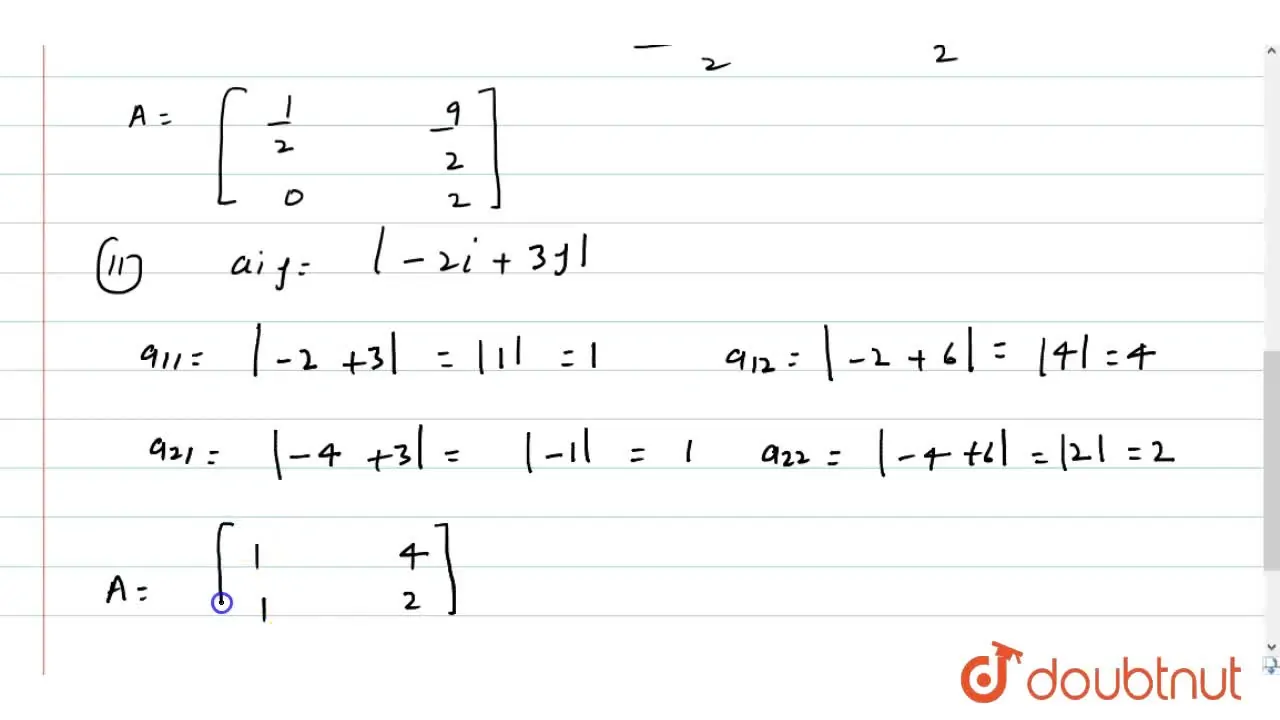Construct a2×2 matrix, where
(i) aij=(i−2j)22 (ii) aij=∣∣−2ˆi+3j∣∣
Video Solution
Text Solution
We know that the notation namely A=[aij]m×n indicates that A is a matrix of order m×n. Also 1≤i≤m,1≤j≤n,i,jεN.
⇒A=(i−2j)22,1≤i≤2,1≤j≤2
a11=(1−2)22=12
∴a11=(1−2)22=92
a21=(2−2×1)22=0
a22=(2−2×2)22=2
Thus, A=[129202]2×2
(ii) Here A=[aij]2×2=|−2i+3ij|,1≤i≤2,1≤j≤2
a11=|−2×1+3×1|=1
a12=|−2×1+3×2|=4
a21=|−2×2+3×1|=1
a22=|−2×2+3×2|=2
A=[1412]2×2
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Construct a 2×2 matrix, where
(i) aij=(i−2j)22 (ii) aij=|−2i+3j|View SolutionComstruct a2×2 matrix, where aij=I−2i+3j∣∣.
View SolutionConstruct a 2×3 matrix whose elements are aij=(i−2j)22.
View SolutionConstruct a 2×2 matrix A=[aij] whose elements aij are given by: (i) aij=(2i+j)22 (ii) aij=|2i−3j|2 (iii) aij=|−3i+j|2
View SolutionConstruct A3×2 matrix whose elements are given by aij=(i+2j).
View SolutionConstruct a matrix [aij]3×3,where aij=i−ji+j.
View SolutionConstruct a2×2 matrix A whose elements are given by aij=12(i−2j)2
View SolutionConstruct a 3×2 matrix whose elements are given by aij=(2i−j).
View SolutionConstruct a matrix [aij]2×2 where aij=i+2j.
View SolutionConstruct a matrix [aij]3×3 , where aij=2i−3j.
View Solution