Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p,q>0. Condition on p and q, so that the maximum of Z occurs at (3, 0) and (1, 1) is ……….Solution in Gujrati
p = 2q
p=q2
p = 3q
p = q
The correct Answer is:B
Step by step video, text & image solution for Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q gt 0. Condition on p and q, so that the maximum of Z occurs at (3, 0) and (1, 1) is ………. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - MULTIPLE CHOICE QUESTIONS42videos
LINEAR PROGRAMMING
- BOOK - KUMAR PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - PRACTICE PAPER - 1214videos
LINEAR PROGRAMMING
- BOOK - KUMAR PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK11videos
LINEAR PROGRAMMING
- BOOK - KUMAR PRAKASHANCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - PRACTICE PAPER - 2 (SECTION - D)2videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - KUMAR PRAKASHANCHAPTER - MATRICES EXERCISE - Practice Paper - 3 (Section - D)1videos
MATRICES
Similar Questions
Solution set of the inequality 2x+y>5 is ………
01:01View SolutionThe correct points of the feasible region determined by the following system of linear inequalities, 2x+y≤10,x+3y≤15,x,y≥0, are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p,q>0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is ..........
02:14View SolutionSolve the following linear programming problem graphically :
Maximise Z = 4x + y …(1)
subject to the constraints :
x+y≤50 …(2)
3x+y≤90…(3)"
x≥0,y≥0 ...(4)03:41View SolutionProve that :
cot−1(√1+sinx+√1−sinx√1+sinx−√1−sinx)=x2,x∈(0,π4)02:06View SolutionFor matrix A=⎡⎢⎣11112−32−13⎤⎥⎦ . Prove that , A3−6A2+5A+11I=0. Hence find A−1 using it .
03:10View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
02:05View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0,10) , (5,5) (25,20),(0,30) Let z = px + qy , where p,q>0 Condition on p and q so that te maximum of z occurs at both the points (25,20 ) and (0,30) is ………
01:35View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
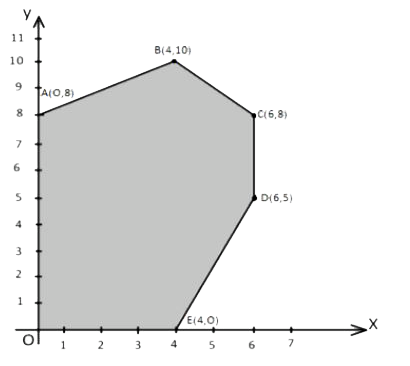
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.02:58View Solutionकिसी राखक व्यवरोधों के निकाय द्वारा निधारित एक सुसंगत क्षत्र क काणाय बिन्दु (0, 3), (1,1) तथा (3, 0) हा मान लीजिए कि Z = px + qy, (जहाँ p,q>0) उद्देश्य फलन है। p तथा q पर लगने वाला वह प्रतिबन्ध, जिससे Z का न्यूनतम मान (3, 0) तथा (1,1) पर प्राप्त होगा।
02:28View SolutionThe vertices of the feasible region determined by some linear constraints are (0,2),(1,1),(3,3),(1,5). Let Z=px+qy where p,q>0. The condition on pandq so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is .......
02:41View SolutionThe corner points of the feasible region determined by some inequality are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p,q>0 condition on p and q so that the maximum of Z occurs at both (15, 15) and (0, 20) is …………
02:37View SolutionThe vertices of the feasible region determined by some linear constraints are (0, 2), (1, 1), (3, 3), (1, 5). Let Z = px + qy where p, q gt 0. The condition on p and q so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is ……..
01:28View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy, where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
01:28View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
01:28View SolutionThe occurs point of the feasible region for an L.P.P. are (0, 3), (1, 1) and (3, 0). If objective function is Z=px+qy,p,q>0, then the condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
01:28View SolutionThe corner points of the feasible region determined by the system linear constraints are (0,10), (5,5), (15,15), (0,20). Let Z = px+ qy, where p, q>0, condition on p and q so that the maximum of Z occurs at both the points (15,15) and (0,20) is
02:06View Solution

