Cube
Cube
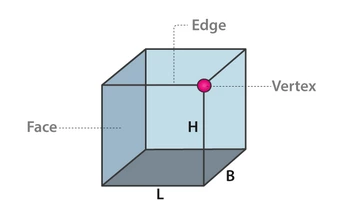
In this lesson, we are going to discuss cube, including the length, surface area and volume. Cube consists of eight vertices, six faces and twelve edges and is a three-dimensional figure. In our daily life, we encounter objects like a tea packet, wooden box, a dice, etc. that have a similar shape. You can notice that all these objects are made of six rectangular planes. You can check the below diagram of a cube to have a better understanding of it.
L = B x H
Look the figure of a cube. You can clearly see the face, edge, and vertex of the cube. Here, L, B and H indicate Length, Breadth and Height respectively. If we look at the length, breadth and height of the cube that represents the edges of the cube, it gets connected in the vertex, which is a single point. The four vertices connect the faces of the cubes.
Length of Diagonal of Cube
Suppose a is the length of the cube then we can define that length of the diagonal of the face of a cube = √2 a
Here, the length of the Diagonal of a Cube = √3 a
Properties of Cube
Coming to the properties of the cube, you should keep in mind that all its faces have got a square shape and they also have equal dimensions as well. Additionally, when it comes to the plane angles of the cube, they are the right angle. Regarding its vertices, it meets the three edges and three faces. It can also be mentioned that the edges which are opposite to each other happen to be parallel.
Surface area of a Cube
We are familiar that for any shape, the area is defined as the region which is occupied by it in a plane. In the case of a cube, it would be in 3d plane when it comes to the area occupied by it. It is required to find out the surface area of the cube as it has got six faces. So, in this case, the formula for the surface area of the cube is:
Surface Area of Cube = 6a2 square units
Volume of a cube
The volume of a cube represents the space that is contained in the cube. For example, if you immerse any object of a cubical shape in the water, then the measurement of the waters in litres that needs to be kept in the objects is calculated by its volume. So, the formula of the volume is:
Volume of cube = a3 cubic units
Related Videos:
Solved Examples
Problem 1: Determine the surface area and volume if the value of the side of the cube is 20cm?
Solution:
Given, side , a = 15cm
Therefore, by the surface area and volume formula of the cube, we can write;
Surface Area = 6a2 = 6 × 152 = 6 × 225.= 1350 cm2
Volume = a3 = 153 = 3375 cm3
Problem 2: A concrete pillar has a height of 25 m. The cross-section of the square of its side is 5 m. Find the cost of the painting of its top and four walls at the rate of Rs 4 per m2?
Solution:
Given:
(l) length = 5 m
(b) breadth = 5 m
(h) height = 25 m
Area of four walls and top
= 2 (l + b)h +lb
= 2( 5 + 5)25 + 5 x 5
= 525 m2
Cost of painting 1m2 = Rs 4
Therefore, the cost of painting 525 m2 =Rs (525 × 4)
= Rs 2100
Problem 3: A tank has an inside dimension of 7 m × 6 m × 5 m. If there is a requirement to line the inside of a rectangular tank on the sides and bottom, then how many m2 would be required?
Solution:
Given:
(l) length = 7 m
(b) breadth = 6 m
(h) height = 5 m
Area of four walls and base
= 2 (l + b)h +lb
= 2(7+ 6)5 + 7 x 6
= 172 m2
Therefore, in order to line the inside of the tank, 172 m2 is required.
Problem 4: The four walls, including the base of a rectangular tank, have dimensions of 4 m × 3 m × 2.5 m. Find out the cost of painting it at the rate of Rs 3.50 per m2
Solution:
Given:
(l) length = 4 m
(b) breadth =3 m
(h) height = 2.5 m
Now, as we know that
Area of four walls and base
= 2 (l + b)h +l
= 2(4+ 3)2.5 + 4 x3
= 47 cm2
Cost of painting 1m2 = Rs 3.50
Therefore, the cost of painting 47 m2 =Rs (31 × 4.50)
= Rs 164.50
Important Chapters:

Similar Questions
Knowledge Check
Following frightening diagrams show identical cubes such that edge of cube 2 lies exactly in the middle of one of the faces of Cube 1 and Cube 4 has a corner at the body centre of the cube 3 . Find the contribution (in fraction) of the spheres shown to each of the cube 1 ,2 , 3 and 4 respectively is
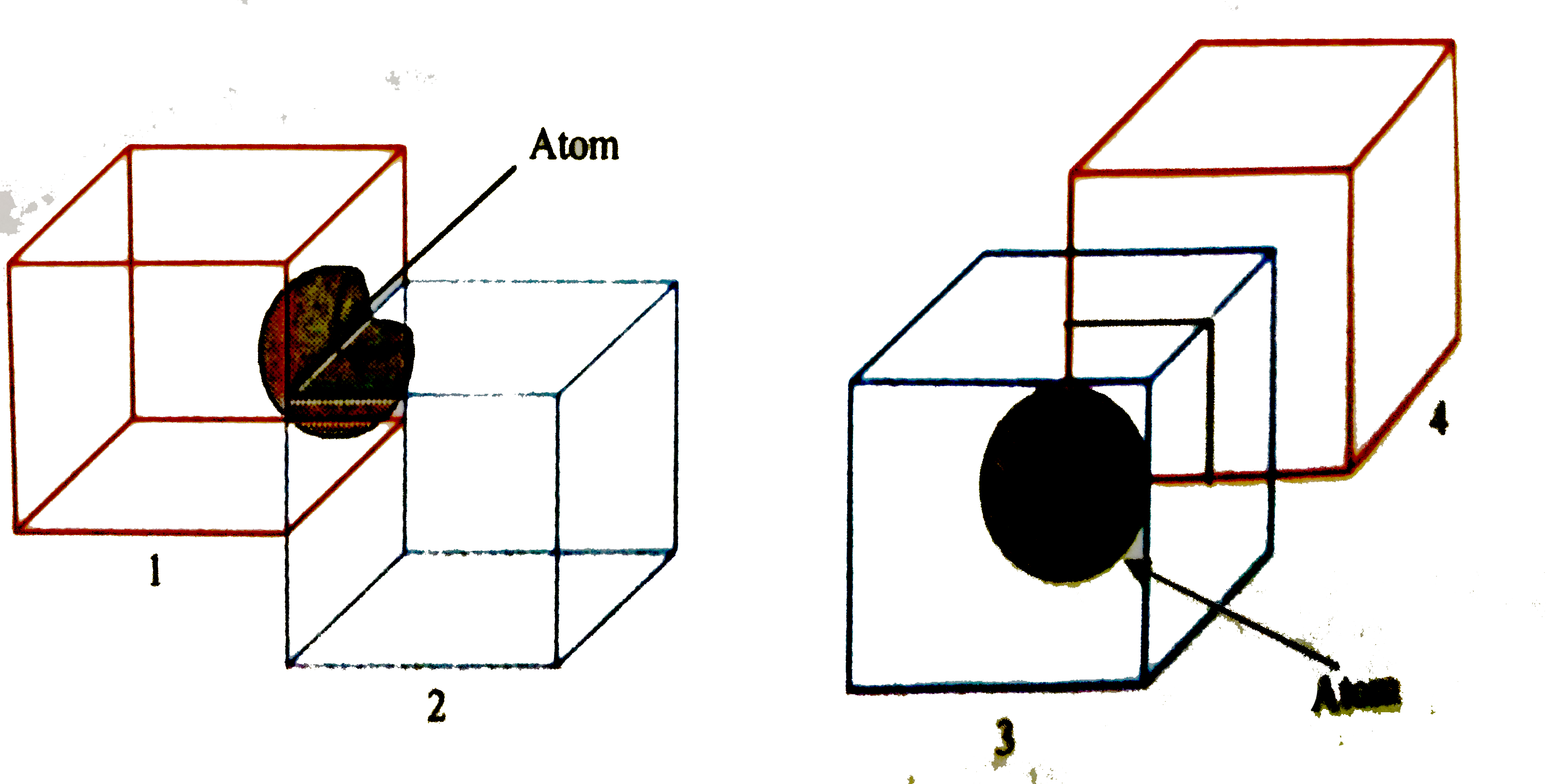 A12,14,1,18B12,14,18,1C18,14,1,12D18,14,12,1
A12,14,1,18B12,14,18,1C18,14,1,12D18,14,12,1Statements :
All spheres are cones
Some cubes are cones
All circles are cubes
Conclusions:
(i) No cube is sphere
(ii) All spheres may be cubes
(iii) Some cones are not circles
(iv) At least some cubes are circles
(v) Some cones which are cubes may be circlesA(i) & (ii) does not followB(i) & (iii) does not followC(ii)& (v) does not followD(iii) & (iv) does not follow

