D is the mid point of side BC and AE⊥BC. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii)b2+c2=2p2+a22Solution in Tamil
Step by step video & image solution for D is the mid point of side BC and AE bot BC. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that (i) b^(2)=p^(2)+ax+(a^(2))/(4) (ii) c^(2)=p^(2)-ax+(a^(2))/(4) (iii) b^(2)+c^(2)=2p^(2)+(a^(2))/(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - ADDITIONAL QUESTIONS SOLVED (MULTIPLE CHOICE QUESTIONS)
23 Videos
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - ADDITIONAL QUESTIONS SOLVED (ANSWER THE FOLLOWING QUESTIONS)
24 Videos
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - EXERCISE 4.5 (MULTIPLE CHOICE QUESTIONS)
15 Videos
- DEPARTMENTAL MODEL PAPER BOOK - FULL MARKSCHAPTER - DEPARTMENTAL MODEL PAPER EXERCISE - PART-IV
3 Videos
- MENSURATION BOOK - FULL MARKSCHAPTER - MENSURATION EXERCISE - ADDITIONAL QUESTIONS SOLVED (iii)
8 Videos
Similar Questions
If a straight line intersects the sides AB and AC of a △ABC at D and E respectively and is parallel to BC , then AEAC= . ………..
View SolutionThe image of man height 1.8m , is of length 1.5 cm on the film of a camera . If the film is 3 cm from the camera, how far is the man from the camera ?
View SolutionIf in triangles ABC and EDF, ABDE=BCFD then they will be similar, when
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionA vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel.
View SolutionProve that identities: ∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣=(ab+bc+ac)3
View SolutionProve |[-bc, b^2+bc, c^2+bc] , [a^2+ac, -ac, c^2+ac] , [a^2+ab, b^2+ab, -ab]|=(ab+bc+ca)^2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BCDE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View SolutionIf a, b, c are in A.P., then prove that :
(i)ab+bc=2b2
(ii) (a−c)2=4(b2−ac)
(iii) a2+c2+4ca=2(ab+bc+ca).
View SolutionIn the given figure, D is the midpoint of side BC and AE⊥BC. If BC=a,AC=b,AB=c,ED=xAD=pandAE=h prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii) (b2+c2)=2p2+12a2
(iv)(b2−c2)=2ax.
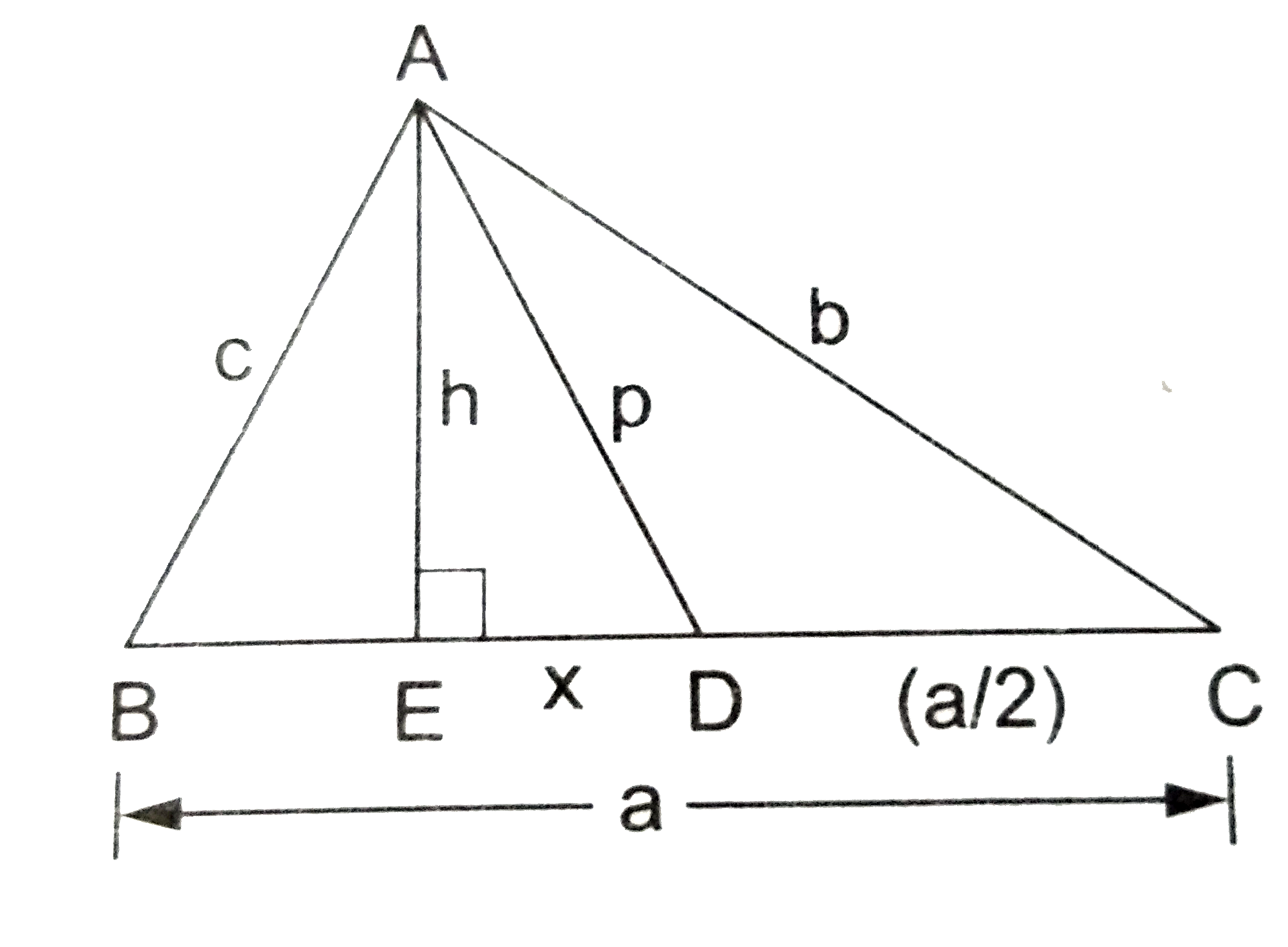
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
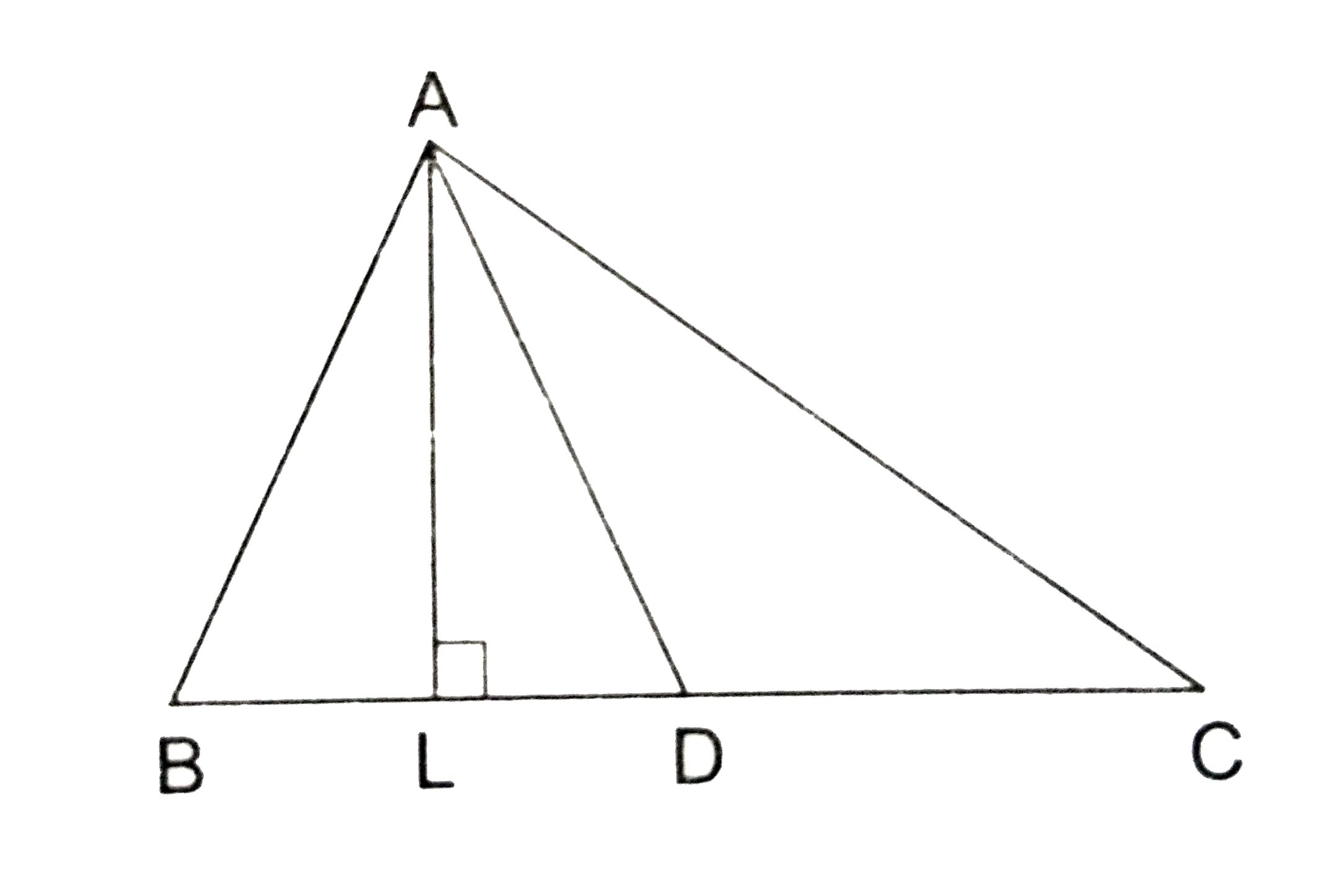
View Solutionएक △ABC में, AC>BD है | D, BC का मध्य बिन्दु है तथा AE⊥BC तो सिद्ध कीजिए कि :
(i) AC2=AD2+BC⋅DE+14BC2
(ii) AB2=AD2−BC⋅DE+14BC2
View Solutionत्रिभुज ABC में D भुजा BC का मध्यबिंदु है और AE⊥BC सिद्ध कीजिए कि
(i) AC2=AD2+BC.DE+14BC2
AB2=AD2−BC.DE+14BC2
View SolutionIf BC =a, AC=b, AB=c , AD=p, DE=x so (i) b ^(2) =p^(2) +ax +1/4 a ^(2) (Ii) c^(2) =p^(2)-ax+1/4 a^(2)
View SolutionD is the mid point of side BC and AE⊥BC. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii)b2+c2=2p2+a22
View SolutionIf a, b, d and p are distinct non - zero real numbers such that (a2+b2+c2)p2−2(ab+bc+cd)p+(b2+c2+d2)≤0 then n. Prove that a, b, c, d are in G. P and ad = bc
View Solution
