Define the collections {E1,E2,E3,...} of ellipses and {R1,R2,R3,...} of rectangles as follows :
E1:x29+y24=1
R1: rectangle of largest area, with sides parallel to the axes, inscribed in E1,
Rn−1,n>1,
Rn : rectangle of largest area, with sides parallel to the axes, inscribed in En>1.
Then which of the following options is /are correct ?
the eccentricities of E18 and E19 are NOT equal.
The distance of a locus from the centre in E9is√532.
N∑n=1(area of Rn)<24, for each positive integer N.
The length of latusrectum of E9is16.
The correct Answer is:C, D
Given equation of ellipse
E1:x29+y24=1 ....(i)
Now, let a vertex of rectangle of largest area with sides parallel to the axes, incribed in E1 be (3cosθ,2sinθ).
So, area of rectangle R1=2(3cosθ)×2(2sinθ)=12sin(2θ)
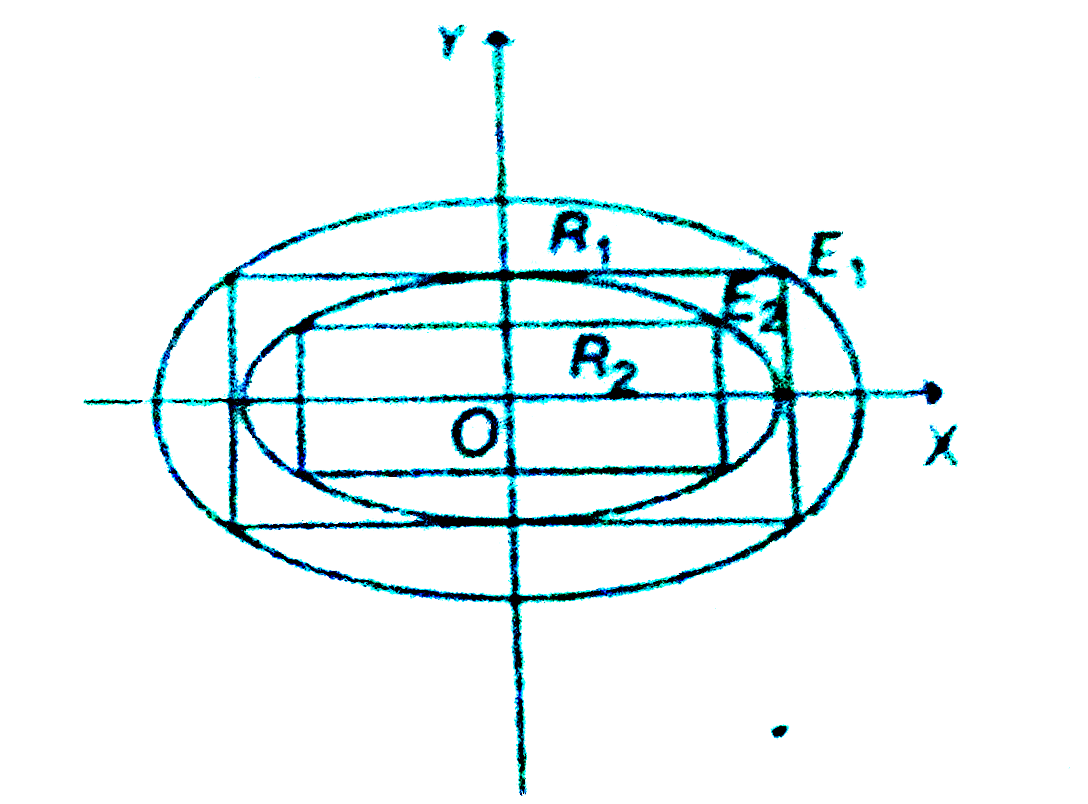
The area of R1 will be maximum, if θ=π4 and maximum area is 12 square units and length of sides of rectangle R1 are 2acosθ=√2a=3√2= length of major axis of ellipse E1 and 2bsinθ=√2b=2√2= length of minor axis of ellipse E2.
So, E2:x2(a√2)2+y2(b√2)2=1 and maxsimum area of rectangle R2=2(a√2)(b√2)
So, En=x2⎛⎝a(√2)n−1⎞⎠2+y2⎛⎝b(√2)n−1⎞⎠2=1, and maximum area of rectangle Rn=2⎛⎜
⎜⎝a(√2)n−1⎞⎟
⎟⎠⎛⎜
⎜⎝b(√2)n−1⎞⎟
⎟⎠
Now option (a),
Since, eccentricity of ellipse En=en=
⎷1(bn)2(an)2
⎷1−⎛⎝b(√2)n−1⎞⎠2⎛⎝a(√2)n−1⎞⎠2=√1−b2a2=√1−45=√53
is independent of π,so eccentricity of E18andE19 are equal.
Option (b), Distance between focus and centre of E9=e.a9
=a(√28)(2)=324×√53=√516unit.
Option (c), ∵n∑n=1(area ofRn)<(area ofR1)+(ara ofR2)+.....∞
<2ab+2ab2+2ab22+......
<2ab(1+12+122+......)
<12(11−1/2)
⇒N∑n=1(area ofRn)<24, each of positive integer N.
Option (d), Length of latusrectum E9=2b29a9=2b2a(√2)8
=2×43×16=16 units.
Hence, option (c) and (d) are correct.
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -1 section-36videos
SOLVED PAPER 2019
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -2 section-18videos
SOLVED PAPER 2019
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -2 section-34videos
SOLVED PAPER 2019
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - RELATION BETWEEN AM,GM, HM AND SOME SPECIAL SERIES34videos
SEQUENCES AND SERIES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - GENERAL EQUATION OF PAIR OF STRAIGHT LINES (Objective Questions I) (Only one correct option)1videos
STRAIGHT LINE AND PAIR OF STRAIGHT LINES
Similar Questions
Define the collection {E1,E2,E3,.....} of ellipses and {R1,R2,R3,.....} of rectangles as follows:
E1=x29+y24=1 ,
R1 : rectangle of largest area, with sides parallel to the axes, inscribed in E1 ,
En : ellipse x2a2n+y2b2n=1 of largest are inscribed in Rn−1,n>1.
then which of the following options is/are corrct?View SolutionFor the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
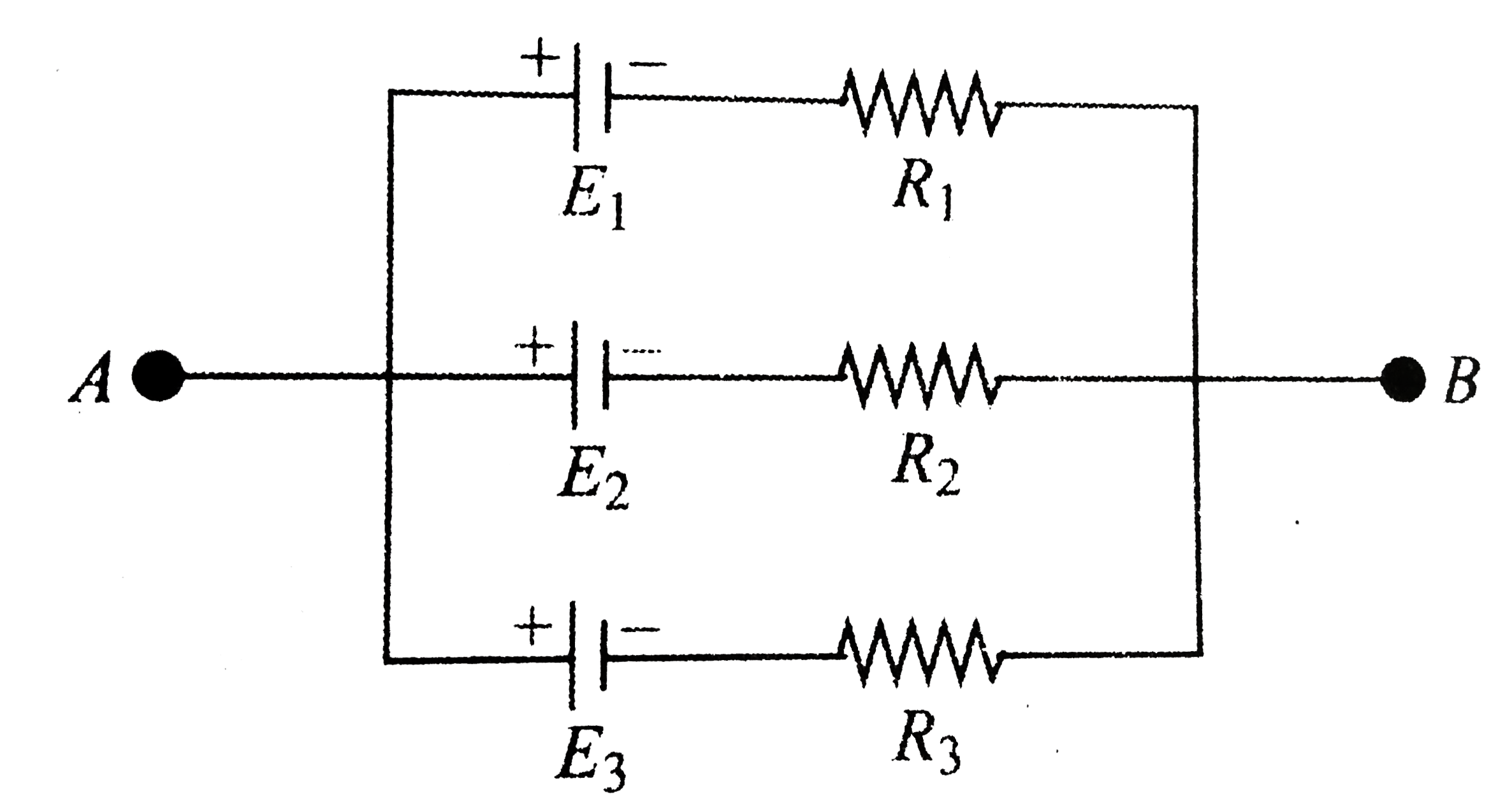 View Solution
View SolutionFor the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
 View Solution
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
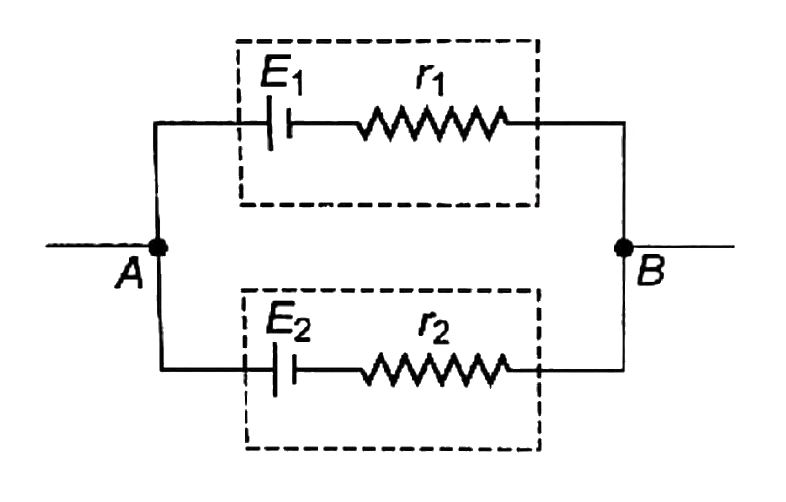 View Solution
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
 View Solution
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinates axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The length (in units) of the major axis of ellipse E2 is
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View SolutionEquation of ellipse E1 is x29+y24=1, A rectangle R1, whose sides are parallel to co-ordinate axes is inscribed in E1 such that its area is maximum now En is an ellipse inside Rn−1 such that its axes is along co-ordinate axes and has maxmim possible area ∀n≥2,n∈N, further Rn is a rectangle whose sides are parallel to co-ordinate axes and is inscribed in En−1. Having maximum area ∀n≥2,n∈N
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View SolutionLet E1andE2 denotes gravitational field at distance r1andr2 from the axis of an infinitely long solid cylinder of the radius R. Which of the following must hold true ?
View Solution

