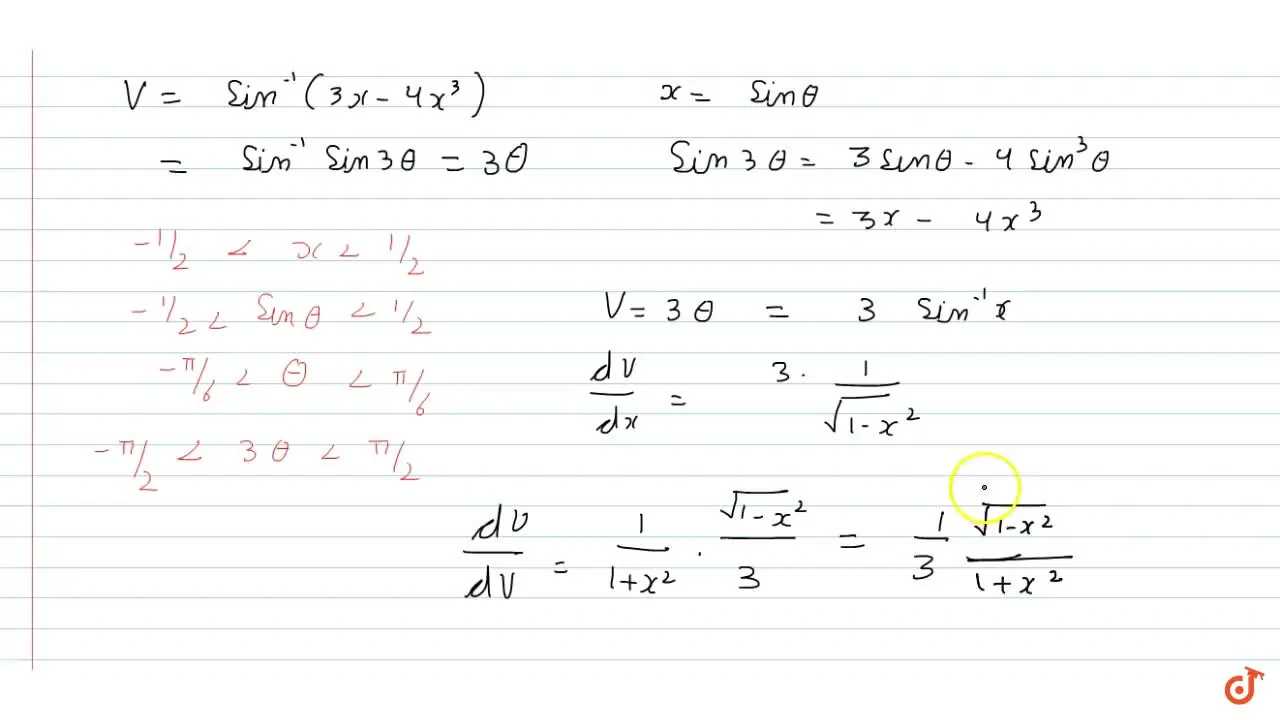Differentiate tan−1(x−1x+1) with respect to sin−1(3x−4x3), if −12<x<12.
Video Solution
Text Solution
Let u=tan−1(x−1x+1) and v=sin−1(3x−4x3)
We need to differentiate u with respect to v that is find dudv.
We have u=tan−1(x−1x+1)
By substituting x=tanθ, we have
u=tan−1(tanθ−1tanθ+1) ⇒u=tan−1(tanθ−tanπ41+tanπ4tanθ) ⇒u=tan−1(tan(θ−π4)) {[∵tan(A−B)=tanA−tanB1+tanAtanB]} Given, −12<x<12⇒{x}∈(−12,12)
However, x=tanθ
⇒tanθ∈(−12,12)
⇒θ∈(tan−1(−12),tan−1(12))
⇒θ∈(−tan−1(12),tan−1(12))
As tan0=0 and tanπ4=1,
we have tan−1(12)∈(0,π4).
Thus, θ−π4 lies in the range of tan−1x.
Hence,
{u}=tan−1(tan(θ−π4))=θ−π4
⇒{u}=tan−1{x}−π4
On differentiating u with respect to x, we get
dudx=ddx(tan−1x−π4)
⇒dudx=ddx(tan−1x)−ddx(π4)
We know ddx(tan−1{x})=11+{x}2 and derivative of a constant is 0 .
⇒dudx=11+x2+0
∴{du}{dx}=11+{x}2
Now, we have v=sin−1(3x−4x3)
By substituting x=sinθ,
we have v=sin−1(3sinθ−4sin3θ)
But, sin3θ=3sinθ−4sin3θ
⇒v=sin−1(sin3θ)
However, x=sinθ
⇒sinθ∈(−12,12)
⇒θ∈(−π6,π6) ⇒3θ∈(−π2,π2) Hence, v=sin−1(sin3θ)=3θ ⇒v=3sin−1x
On differentiating v with respect to x, we get
dvdx=ddx(3sin−1x)
⇒dvdx=3ddx(sin−1x)
We know
ddx(sin−1x)=1√1−x2
⇒dvdx=3×1√1−x2
∴dvdx=3√1−x2
We have
dudv=dudxdvdx
⇒dudv=11+x23√1−x2
⇒dudv=11+x2×√1−x23
∴dudv=√1−x23(1+x2)
Thus,
dudv=√1−x23(1+x2)
|
Updated on:21/07/2023
Related Playlists
- BOOK - RD SHARMACHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Solved Examples And Exercises102videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
- BOOK - RD SHARMACHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - Solved Examples And Exercises67videos
DIRECTION COSINES AND DIRECTION RATIOS
Similar Questions
Differentiate tan−1(x−ax+a) with respect to x
View SolutionDifferentiate tan−1(a+x1−ax) with respect to x
View SolutionDifferentiate tan−1(11−x+x2)
View SolutionDifferentiate tan−1(1+cosxsinx) with respect to x
View SolutionDifferentiate tan−1(2x+11−4x) with respect to x.
View SolutionDifferentiate √tan−1(x2) with respect to x :
View SolutionDifferentiate tan−1(cosx1+sinx) with respect to sec−1x.
View SolutionDifferentiate tan−1[√1+x2−1x] with respect to x
View SolutionDifferentiate tan−1(√1+x2−1x) with respect to tan−1x,x≠0.
View SolutionDifferentiate tan−1(2x1−x2) with respect to x , if x∈(−1, 1)
View Solution