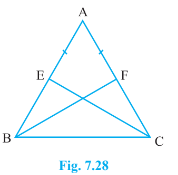
E and F are respectively the mid-points of equal sides AB and AC of ΔABC (see Fig. 7.28). Show that BF\ =\ CE .
The correct Answer is:CE
Step by step video solution for E and F are respectively the mid-points of equal sides AB and AC of DeltaA B C (see Fig. 7.28). Show that B F"\ "="\ "C E . by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
E and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
View SolutionD, E and F are respectively the mid -points of the sides BC, CA and AB of a △ABC .Show that (i) BDEF is a parallelogram
View SolutionIf D, E and F are respectively, the mid-points of AB, AC and BC in ΔABC, then BE + AF is equal to
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)
View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of △ABC. Find the ratio of the areas of △DEF and △ABC.
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View Solution
