E is the mid-point of side AB and F is the mid point of side DC of parallelogram ABCD . Prove that AEFD is a parallelogram.
To prove that AEFD is a parallelogram, we will use the properties of a parallelogram and the midpoints of the sides of the given parallelogram ABCD.
1. Identify the midpoints:
Let E be the midpoint of side AB and F be the midpoint of side DC in parallelogram ABCD.
2. Use the midpoint theorem:
According to the midpoint theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half as long.
3. Apply the theorem to triangles:
In triangles ABE and CDF, since E and F are midpoints:
- EF is parallel to AC and EF = 1/2 AC.
- AE is parallel to DF and AE = 1/2 DC.
4. Show that opposite sides are equal:
Since ABCD is a parallelogram, we know that AB is equal to DC (AB = DC). Therefore, AE = 1/2 AB and DF = 1/2 DC implies that AE = DF.
5. Show that opposite sides are parallel:
From the midpoint theorem, we have established that:
- EF is parallel to AC.
- AE is parallel to DF.
6. Conclude that AEFD is a parallelogram:
Since both pairs of opposite sides (AE and DF, EF and AC) are equal and parallel, we conclude that AEFD is a parallelogram.
Final Statement:
Thus, we have proved that AEFD is a parallelogram.
Let E be the midpoint of side AB and F be the midpoint of side DC in parallelogram ABCD.
According to the midpoint theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half as long.
In triangles ABE and CDF, since E and F are midpoints:
- EF is parallel to AC and EF = 1/2 AC.
- AE is parallel to DF and AE = 1/2 DC.
Since ABCD is a parallelogram, we know that AB is equal to DC (AB = DC). Therefore, AE = 1/2 AB and DF = 1/2 DC implies that AE = DF.
From the midpoint theorem, we have established that:
- EF is parallel to AC.
- AE is parallel to DF.
Since both pairs of opposite sides (AE and DF, EF and AC) are equal and parallel, we conclude that AEFD is a parallelogram.
Thus, we have proved that AEFD is a parallelogram.
Topper's Solved these Questions
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - POLYGONS - 3 MARKS QUESTIONS
5 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - POLYGONS - 4 MARKS QUESTIONS
4 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(B)
16 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- SIMULTANEOUS EQUATIONSBOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)
13 Videos
Similar Questions
X and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Prove that □AXCY is a parallelogram.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
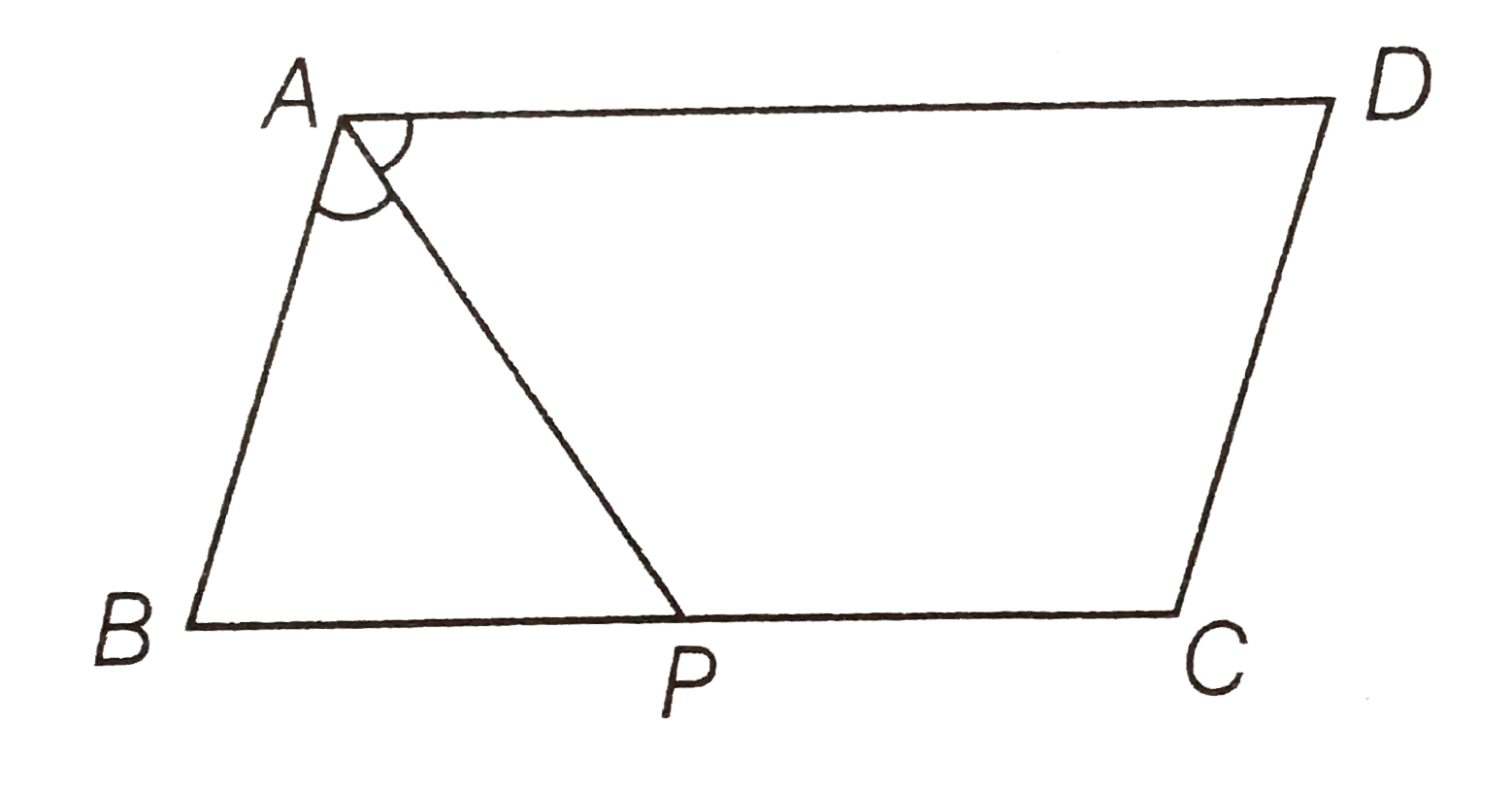
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
View SolutionIn triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
View SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View SolutionIn triangle ABC, D and E are mid-points of sides AB and BC respectively. Also, F is a point in side AC so that DF is parallel to BC
(i) Prove that DBEF is a parallelogram.
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2EA and F is a point on DC such that DF=2 FC. Prove that AECF is a parallelogram whose area is one third area of parallelogram ABCD.
View SolutionE,F,G,H are respectively, the mid-points of the sides of parallelogram ABCD . Show that the area of EFGH is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join H and F
View SolutionIn ΔABC, E is mid-point of side AB and EBCD is a parallelogram. If the area of ΔABC is 80 cm, find the area of parallelogram EBCD.
View Solution
