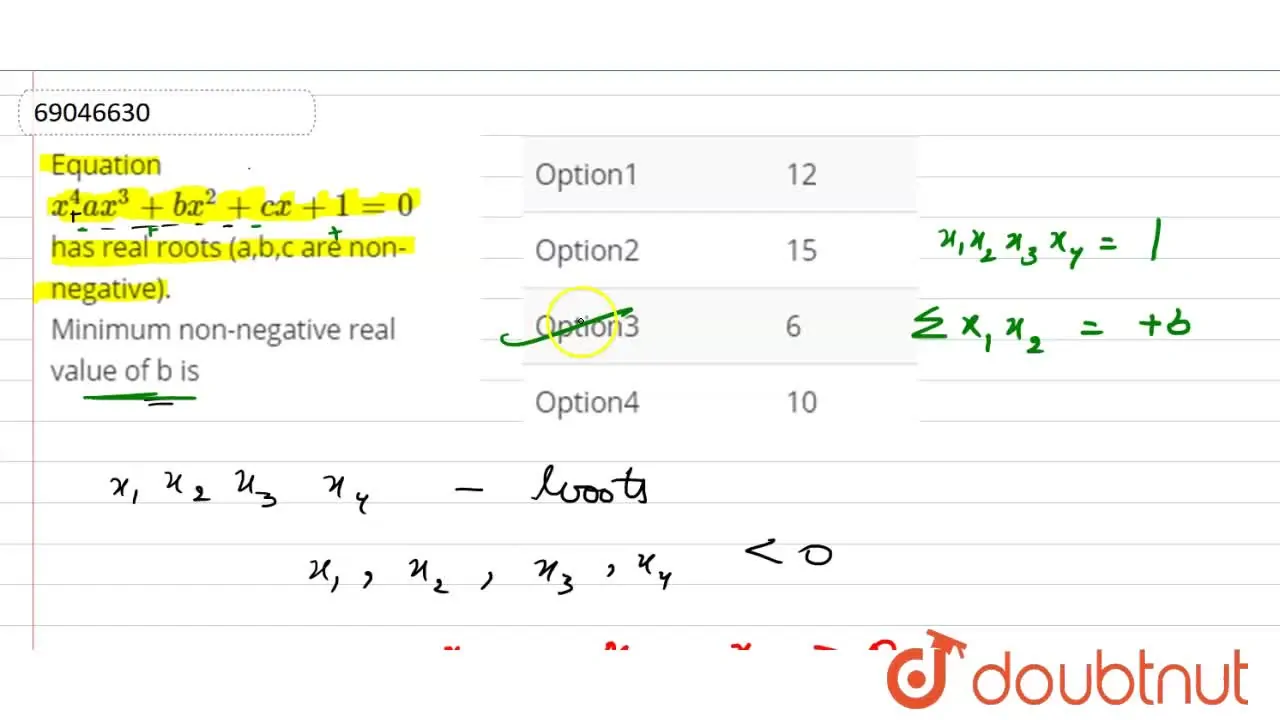
Equation has real roots (a,b,c are non-negative).
Minimum non-negative real value of b is
12
15
6
10
The correct Answer is:C
Since, a,b,c 0 roots must be negative. Let the roots be
. Then.
Now,
Hence, the minimum value of a is 4. similarly,
or
Hence, the minimum value of is 6. Finally
or c ge 4
Hence, the minimum value of c is 4.
Related Playlists
- BOOK - CENGAGECHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Exercise (Numerical) & JEE Previous Year11videos
INEQUALITIES INVOLVING MEANS
- BOOK - CENGAGECHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Exercise (Multiple)5videos
INEQUALITIES INVOLVING MEANS
- BOOK - CENGAGECHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer21videos
INEQUALITIES AND MODULUS
- BOOK - CENGAGECHAPTER - INTEGRALSEXERCISE - Solved Examples And Exercises324videos
INTEGRALS
Similar Questions
Equation x4ax3+bx2+cx+1=0 has real roots (a,b,c are non-negative).
Minimum non-negative real value of a isView SolutionEquation x4+ax3+bx2+cx+1=0 has real roots (a,b,c are non-negative). Minimum non-negative real value of c is
View SolutionThe quadratic equation ax2+bx+c=0 has real roots if:
View SolutionIf the equation x4+ax3+2x2+bx+1=0 has at least one real root (a,b∈R) then the minimum value of a2+b2
View SolutionRoots are real only when D is non-negative.
View SolutionStatement -1 ax3+bx+c=0 where a,b,cεR cannot have 3 non-negative real roots.
Statement 2 Sum of roots is equal to zero.View Solutionax2+2bx−3c=0 has no real root and a+b>3c4 then
View SolutionIf the equation ax2+bx+c=0andcx2+bx+a=0a≠c, have negative common root then the value of a-b+c is
View SolutionIf the equation cx2+bx−2a=0 has no real roots and a<b+c2 then
View SolutionIf the equation cx2+bx−2a=0 has no real roots and a<b+c2 then
View Solution