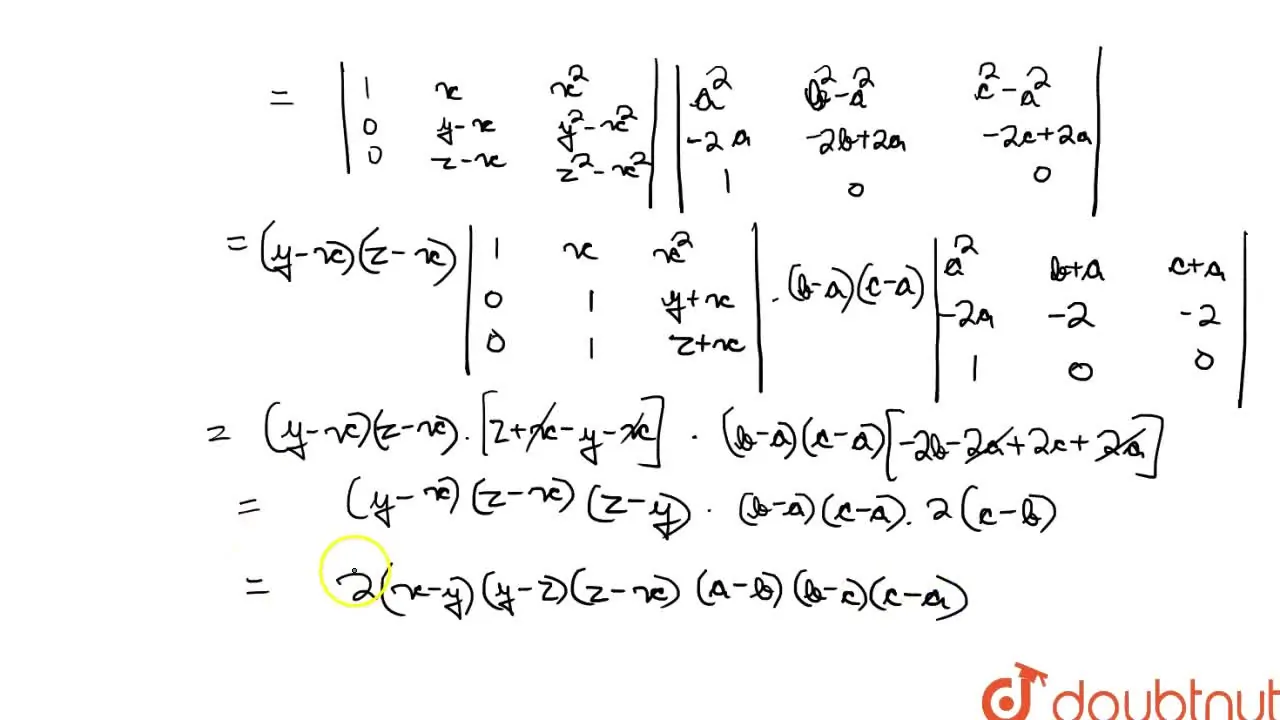Express Δas a product to two deteminants and then find its value.
Δ=∣∣
∣
∣∣(a−x)2(b−x)2(c−x)2(a−y)2(b−y)2(c−y)2(a−z)2(b−z)2(c−z)2∣∣
∣
∣∣
To find out which two determinants when multiplied yield the above dterminaint, expres each element as a sum of three numbers, each of which is a product of two number.
Observe that
(a−x)2=a2−2ax+x2=(1)(a2)+(x)(−2a)+(x2)(1)
(b−x)2=a2−2ax+x2=(1)(a2)+(x)(−2a)+(x2)(1)
(c−x)2=a2−2ax+x2=(1)(a2)+(x)(−2a)+(x2)(1)
Write Δ as
Δ=∣∣
∣
∣∣1xx21yy21zz2∣∣
∣
∣∣∣∣
∣
∣∣a2−2a1b2−2b1c2−2c1∣∣
∣
∣∣(Row-by-row multiplication)
=2∣∣
∣
∣∣1xx21yy21zz2∣∣
∣
∣∣∣∣
∣
∣∣1aa21bb21cc2∣∣
∣
∣∣
=2(x−y)(y−z)(a−b)(b−c)(c−a)
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - DETERMINANTS EXERCISE - Try Yourself12videos
DETERMINANTS
- BOOK - AAKASH INSTITUTECHAPTER - DETERMINANTS EXERCISE - SECTION A33videos
DETERMINANTS
- BOOK - AAKASH INSTITUTECHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - section - J6videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - AAKASH INSTITUTECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment Section - J (Aakash Challengers Questions)4videos
DIFFERENTIAL EQUATIONS
Similar Questions
Without expanding, show that Delta=∣∣(a−x)2(a−y)2(a−z)2(b−x)2(b−y)2(b−z)2(c−x)2(c−y)2(c−z)2∣∣=2(a−b)(b−c)(c−a)(x−y)(y−z)(z−x)
View SolutionProve that the value of each the following determinants is zero: ∣∣ ∣ ∣∣(ax+a−x)2(ax−a−x)21(by+b−y)2(by−+b−y)21(cz+c−z)2(cz−c−z)21∣∣ ∣ ∣∣
View SolutionIf a,b,c>0 and x,y,z∈R then the determinant: ∣∣ ∣ ∣∣(ax+a−x)2(ax−a−x)21(by+b−y)2(by−b−y)21(cz+c−z)2(cz−c−z)21∣∣ ∣ ∣∣ is equal to
View SolutionThe value of Δ=∣∣ ∣ ∣∣(ax+a−x)2(ax−a−x)21(ay+a−y)2(ay−a−y)21(az+a−z)2(az−a−z)21∣∣ ∣ ∣∣, is
View SolutionIf a,b,c>0 and x,y,z∈R then ∣∣ ∣ ∣∣(ax+a−x)2(ax−a−x)21(by+b−y)2(by−b−y)21(cz+c−z)2(cz−c−z)21∣∣ ∣ ∣∣=
View SolutionShow that ∣∣ ∣ ∣∣1xx21yy21zz2∣∣ ∣ ∣∣∣∣ ∣ ∣∣a212ab212bc212c∣∣ ∣ ∣∣=∣∣ ∣ ∣∣(a−x)2(b−x2)(c−x)2(a−y)2(b−y)2(c−y)2(a−z)2(b−z)2(c−z)2∣∣ ∣ ∣∣
View Solutionprove that ∣∣ ∣ ∣∣(a−x)2(a−y)2(a−z)2(b−x)2(b−y)2(b−z)2(c−x)2(c−y)2(c−z)2∣∣ ∣ ∣∣
∣∣ ∣ ∣∣(1+ax)2(1+bx)2(1+cx)2(1+ay)2(1+by)2(1+cy)2(1+az)2(1+bx)2(1+cz)2∣∣ ∣ ∣∣
=2(b−c)(c−a)(a−b)×(y−z)(z−x)(x−y)View SolutionIf Δ=∣∣ ∣ ∣∣x2y−z−zy2x−z−zy2y−z2x−2y−z∣∣ ∣ ∣∣,then
View SolutionIf a,b,c>0&x,y,z∈R then the determinant⎡⎢ ⎢ ⎢⎣(ax+a−x)2(ax−a−x)21(by+b−y)2(by−b−y)21(cz+c−z)2(cz−c−z)21⎤⎥ ⎥ ⎥⎦=
View SolutionIf x=asecθcosθ,y=bsecθsinθandz=θtanθ, then find the value of x2a2+y2b2−z2c2
View Solution