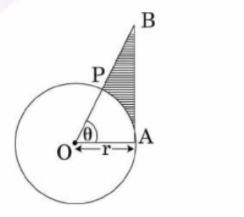
Fig. 15.17, shows a sector of a circle, centre O , containing an angle θo , prove that: (FIGURE) (i) Perimeter of the shaded region is r (tanθ+secθ+πθ180−1) (ii) Area of the shaded region is r22 (tanθ−πθ180)
To solve the problem, we need to prove two statements about the shaded region in the sector of a circle. Let's denote the radius of the circle as r and the angle of the sector as θ (in degrees).
Part (i): Proving the Perimeter of the Shaded Region
1. Identify the Components of the Perimeter:
- The perimeter of the shaded region consists of:
- The arc AC
- The line segment AB
- The line segment BC
2. Calculate the Length of Arc AC:
- The length of an arc in a circle is given by the formula:
Arc Length=θ360×2πr
- Therefore, for arc AC:
Arc AC=θπr180
3. Calculate the Length of Segment AB:
- In the right triangle OAB, we can use the definition of tangent:
tan(θ)=OppositeAdjacent=ABOA
- Since OA=r:
AB=rtan(θ)
4. Calculate the Length of Segment BC:
- The length of segment BC can be calculated as:
BC=OB−OC
- Here, OB=rsec(θ) (since OB is the hypotenuse of triangle OAB) and OC=r (the radius).
- Thus:
BC=rsec(θ)−r=r(sec(θ)−1)
5. Combine All Parts to Find the Perimeter:
- The total perimeter P of the shaded region is:
P=Arc AC+AB+BC
- Substituting the values we found:
P=θπr180+rtan(θ)+r(sec(θ)−1)
- Simplifying:
P=rtan(θ)+rsec(θ)+θπr180−r
- Therefore, we can express the perimeter as:
P=r(tan(θ)+sec(θ)+θπ180−1)
Conclusion for Part (i):
Thus, we have proved that the perimeter of the shaded region is:
P=r(tan(θ)+sec(θ)+θπ180−1)
---
Part (ii): Proving the Area of the Shaded Region
1. Identify the Components of the Area:
- The area of the shaded region consists of:
- The area of triangle OAB
- The area of the sector OAC
- The area of the shaded region can be expressed as:
Area=Area of Sector OAC−Area of Triangle OAB
2. Calculate the Area of Sector OAC:
- The area of a sector is given by:
Area of Sector=θ360×πr2
- Thus:
Area of Sector OAC=θπr2360
3. Calculate the Area of Triangle OAB:
- The area of triangle OAB can be calculated using the formula:
Area=12×base×height
- Here, the base OA=r and height AB=rtan(θ):
Area of Triangle OAB=12×r×(rtan(θ))=r2tan(θ)2
4. Combine the Areas to Find the Area of the Shaded Region:
- The area of the shaded region is:
Area=Area of Sector OAC−Area of Triangle OAB
- Substituting the values we found:
Area=θπr2360−r2tan(θ)2
- To express this in a simplified form:
Area=r22(tan(θ)−πθ180)
Conclusion for Part (ii):
Thus, we have proved that the area of the shaded region is:
Area=r22(tan(θ)−πθ180)
---
- The perimeter of the shaded region consists of:
- The arc AC
- The line segment AB
- The line segment BC
- The length of an arc in a circle is given by the formula:
Arc Length=θ360×2πr
- Therefore, for arc AC:
Arc AC=θπr180
- In the right triangle OAB, we can use the definition of tangent:
tan(θ)=OppositeAdjacent=ABOA
- Since OA=r:
AB=rtan(θ)
- The length of segment BC can be calculated as:
BC=OB−OC
- Here, OB=rsec(θ) (since OB is the hypotenuse of triangle OAB) and OC=r (the radius).
- Thus:
BC=rsec(θ)−r=r(sec(θ)−1)
- The total perimeter P of the shaded region is:
P=Arc AC+AB+BC
- Substituting the values we found:
P=θπr180+rtan(θ)+r(sec(θ)−1)
- Simplifying:
P=rtan(θ)+rsec(θ)+θπr180−r
- Therefore, we can express the perimeter as:
P=r(tan(θ)+sec(θ)+θπ180−1)
Thus, we have proved that the perimeter of the shaded region is:
P=r(tan(θ)+sec(θ)+θπ180−1)
- The area of the shaded region consists of:
- The area of triangle OAB
- The area of the sector OAC
- The area of the shaded region can be expressed as:
Area=Area of Sector OAC−Area of Triangle OAB
- The area of a sector is given by:
Area of Sector=θ360×πr2
- Thus:
Area of Sector OAC=θπr2360
- The area of triangle OAB can be calculated using the formula:
Area=12×base×height
- Here, the base OA=r and height AB=rtan(θ):
Area of Triangle OAB=12×r×(rtan(θ))=r2tan(θ)2
- The area of the shaded region is:
Area=Area of Sector OAC−Area of Triangle OAB
- Substituting the values we found:
Area=θπr2360−r2tan(θ)2
- To express this in a simplified form:
Area=r22(tan(θ)−πθ180)
Thus, we have proved that the area of the shaded region is:
Area=r22(tan(θ)−πθ180)
Topper's Solved these Questions
Similar Questions
Figure shows a sector of a circle of radius r containing an angle θ∘ The area of the sector is Acm2 and the perimeter is 50cm. Prove that θ=360π(25r−1) and A=25r−r2
View SolutionIn the given figure, is shown a sector OAP of a circle with centre 0, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tanθ+secθ+πθ180−1]
View Solution
Knowledge Check
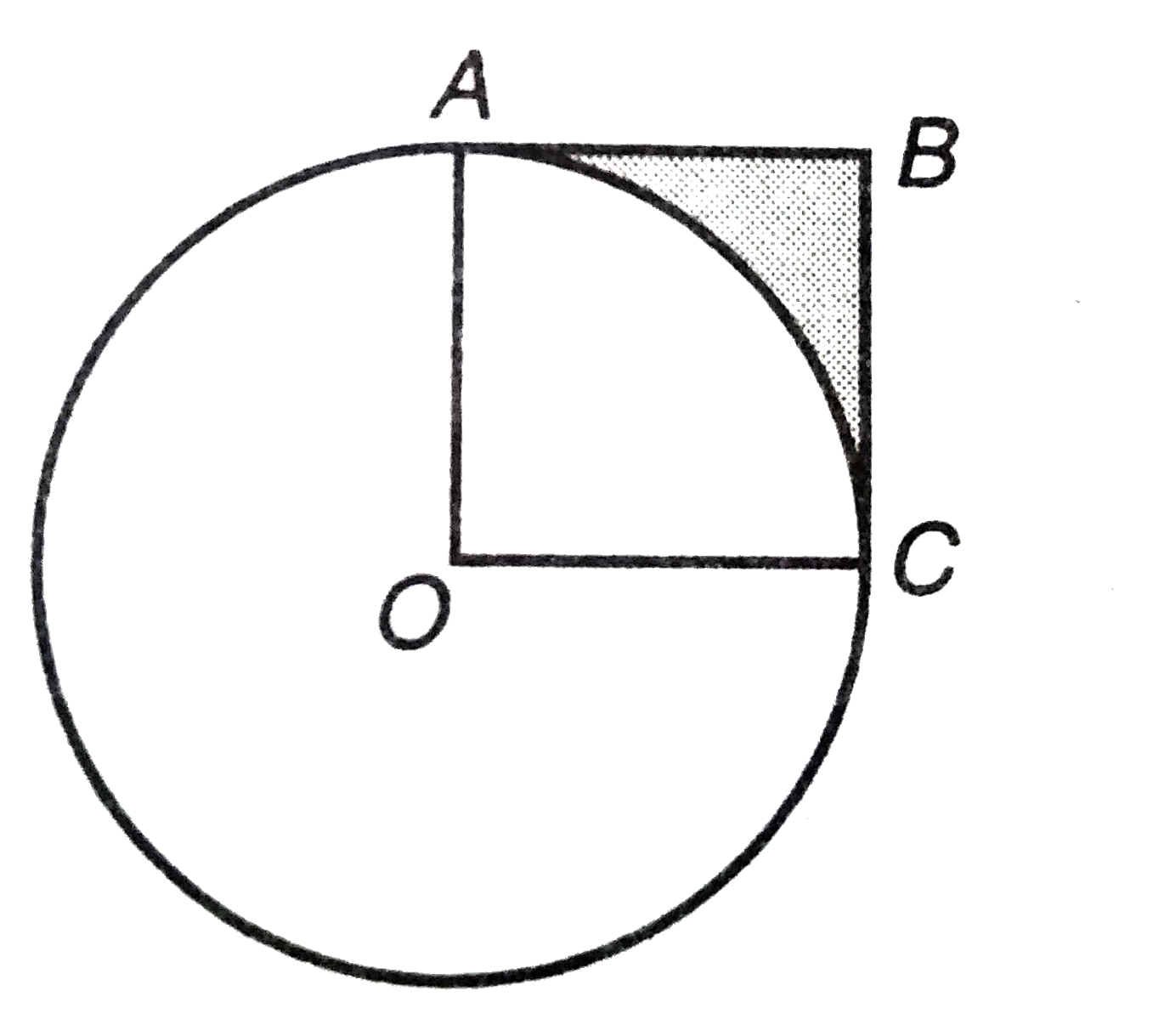
In the figure above, OABC is a square. If the area of circle O is 2π, what is the area of the shaded region?Aπ2−1B2−π2Cπ−2Dπ−12
In the figure above, Radius of circle is 8 and angle formed by sector at center is 120∘ , what is the area of the shaded region ?A16π3−16√3B16π3−16C16π3−64√3D64π3−16√3
In the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn figure, three sectors of a circle of radius 7 cm, making angles of 60∘,80∘ and 40∘ at the center are shaded. Find the area of the shaded region.
View SolutionBE and CD are both diameters of circle with centre A (see figure). If the area of the circle is 180units2, what is the total area of the shaded regions?
View SolutionIf Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.

View SolutionIn Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.
View SolutionIn figure arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region .

View Solution
