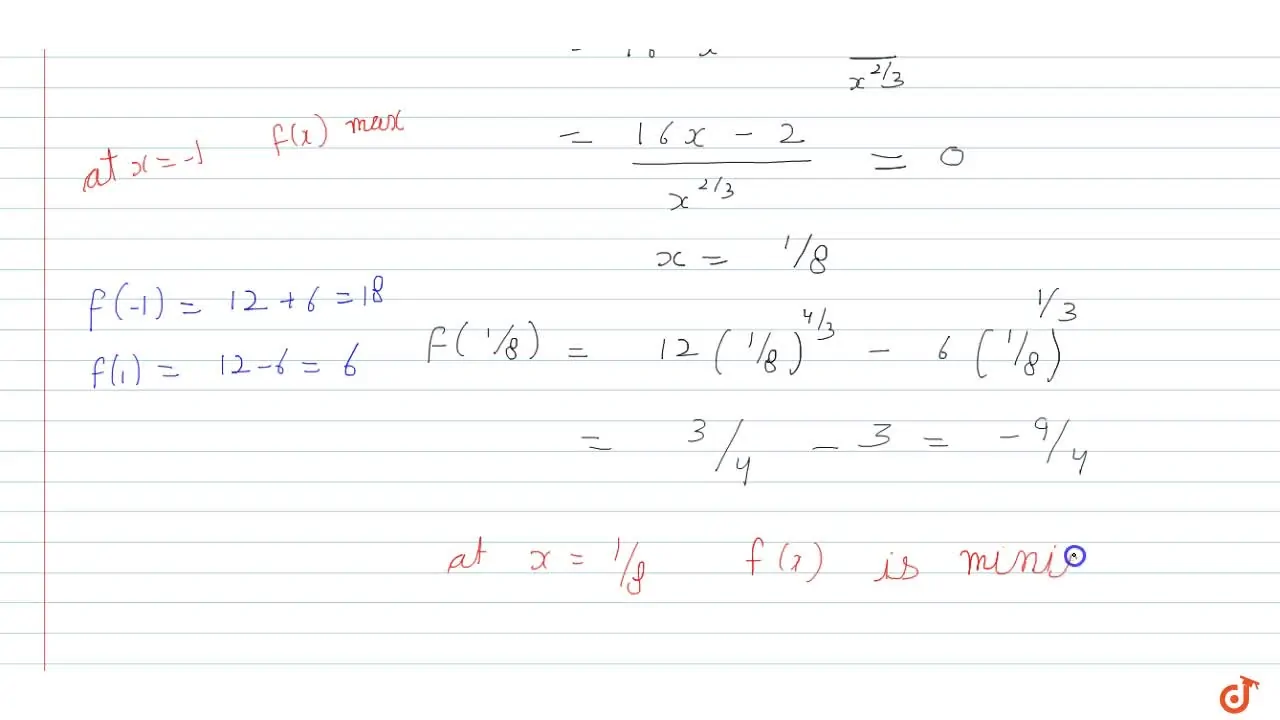Find absolute maximum and minimum values of a function f given by f(x)=12x43−6x13,x∈[−1,1].
Here, f(x)=12x43−6x13
f'(x)=16x13−2x−23=16x13−2x23=16x−2x23
Now, for maximum and minimum value,
f'(x)=0
∴16x−2x23=0
⇒16x−2=0
⇒x=18
So, f(18)=12(18)43−6(18)13
=34−3=−94
∴f(18)=−94
Now, we will check f(x) at boundaries (1,−1).
f(−1)=12(1)−6(−1)=18
f(1)=12(1)−6(1)=12
So, clearly, f(x) will be minimum at x=18 and maximum at x=−1.
So, minimum value of f(x) is −94 and maximum value is 18.
Similar Questions
Find absolute maximum and minimum values of a function f given by f(x)=12x4/3−6x1/3, x∈[−1, 1] .
View SolutionFind absolute maximum and minimum values of a function f given by f(x)=12x43−6x13,x∈[−1,1].
View SolutionFind the maximum and minimum value if any , of the function f given by f(x)=x6−5.
View SolutionFind the absolute maximum and minimum values of a function f given by
f(x)=2x3−15x2+36x+1 on the interval [1,5].View SolutionFind the absolute maximum and minimum values of a function f given by f(x)=2x3−15x2+36x+1 on the interval [1, 5] .
View SolutionFind the maximum and minimum values of any of the function f given by f(x)=x4,x∈R .
View SolutionFind the maximum and minimum values , if any , of the function f given by f(x)=3−|x|
View SolutionFind the absolute maximum and absolute minimum vlaues of a function f given by f(x)=2x3−15x2+36x+3 on the interval [0,6] .
View SolutionFind the absolute maximum and minimum values of the function f given by f(x)=cos2x+sinx,x∈[0,π]
View SolutionFind the maximum and minimum value if any , of the function f given by f(x)=5−|x−1|.
View Solution