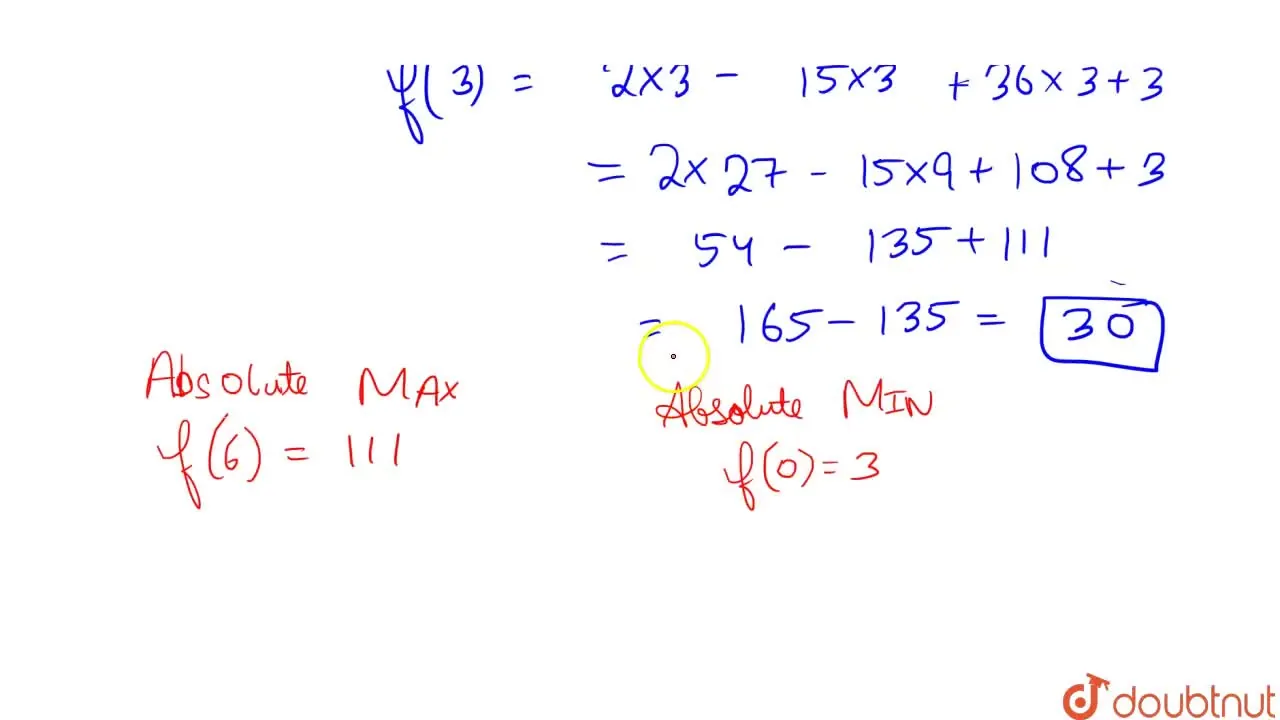Find the absolute maximum and absolute minimum vlaues of a function f given by f(x)=2x3−15x2+36x+3 on the interval [0,6] .
We have f(x)=2x3−15x2+36x+3
f'(x)=6x2−30x+36
=6(x−3)(x−2)
For maxima and minima
f'(x)=0
(x-2)(x-3)=0
x=2,3
Now using rule to find absolute maxima and absolute minima
f(0)=3
f(x)=2(2)3−15(2)2+36(2)+3=31
f(3)=2(3)3−15(3)2+36(3)+3=30
f(6)=2(6)3−15(6)2+36×6+3=111
Hence Absolute maxima of function =f(6)=111
Absolute minima of function =f(0)=3
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - TRY YOURSELF39videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-A (Competition Level Questions)50videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTECHAPTER - APPLICATION OF INTEGRALS EXERCISE - Assignment Section - I Aakash Challengers Questions2videos
APPLICATION OF INTEGRALS
Similar Questions
Find the absolute maximum and absolute minimum vlaues of a function f given by f(x)=2x3−33x22+36x+2 on the interval [−1,9].
View SolutionFind the absolute maximum and minimum values of a function f given by
f(x)=2x3−15x2+36x+1 on the interval [1,5].View SolutionFind the absolute maximum and minimum values of a function f given by f(x)=2x3−15x2+36x+1 on the interval [1, 5] .
View SolutionFind absolute maximum and minimum values of a function f given by f(x)=12x4/3−6x1/3, x∈[−1, 1] .
View SolutionFind the absolute maximum and the absolute minimum value of the function given by :
f(x)=sin2x−cosx,x∈[0,π].View SolutionFind the absolute maximum and minimum values of the function f given by f(x)=cos2x+sinx,x∈[0,π]
View SolutionFind the absolute maximum and minimum values of the function f given by f(x)=cos2x+sinx , x∈[0, π] .
View SolutionFind absolute maximum and minimum values of a function f given by f(x)=12x43−6x13,x∈[−1,1].
View SolutionFind the absolute maximum and absolute minimum values of f(x)=(x−1)2+3 in [−3, 1]
View SolutionFind the maximum and minimum values of the function :
f(x)=2x3−15x2+36x+11.View Solution