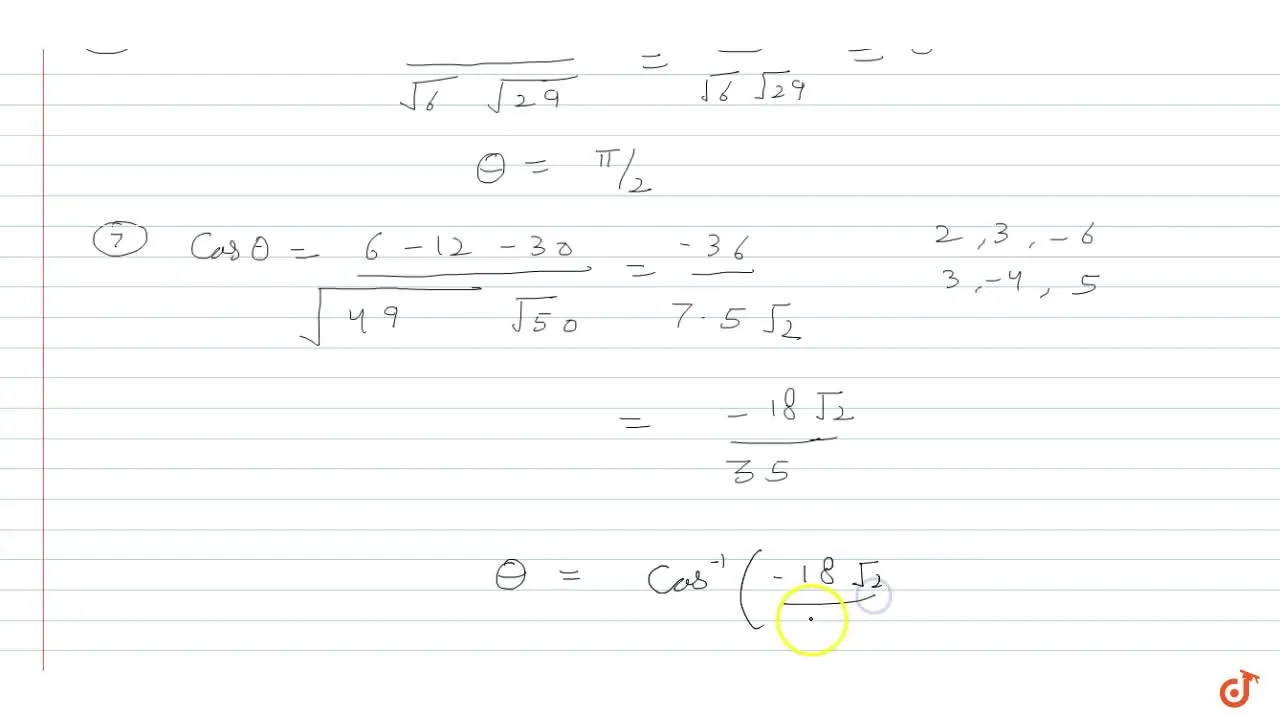Find the angle between the vectors whose direction cosines are proportional to 2,3,−6 and 3,−4,5.
Let the required angle is θ.
Then,
cosθ=l1l2+m1m2+n1n2√l21+m21+n21√l22+m22+n22
Putting given values of direction cosines,
cosθ=2⋅3+3⋅(−4)+(−6)⋅5√22+32+(−6)2√32+(−4)2+52
⇒cosθ=6−12−307√50
⇒cosθ=−3635√2
⇒θ=cos−1(−18√235).
Related Playlists
Similar Questions
The angle between the lines whose direction cosines are proportional to (1,2,1) and (2,-3,6) is
View SolutionWhat is the angle between the lines whose direction cosines are proportional to (2,3,4) and (1,-2,1) respectively?
View SolutionWhat is the angle between the lines whose direction cosines are proportional to (2,3,4)and(1,−2,1) respectively
View SolutionFind the angle between the vectors with direction ratios proportional to 1,−2,1 and 4,3,2.
View SolutionFind the angle between the vectors with direction ratios proportional to 4,−3,5 and 3,4,5.
View SolutionFind the acute angle between the lines whose direction ratios are proportional to 2:3:6 and 1:2:2.
View SolutionWrite the angle between the lines whose direction ratios are proportional to 1, -2, 1 and 4, 3, 2.
View SolutionFind the angel between the vectors with direction ratios proportional to 1, -2, 1 and 4, 3, 2.
View SolutionFind the angle between two lines whose direction ratios are proportional to 1,1,2and(√3−1),(−√3−1),4 .
View SolutionFind the angle between the pairs of lines with direction ratio proportional to: 5, -12, 13 and -3, 4, 5
View Solution