Find the area of the greatest rectangle that can be inscribed in the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 .$

A

$\frac{a}{b}$

B

$\sqrt{a b}$

C

$a b$

D

$2 a b$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

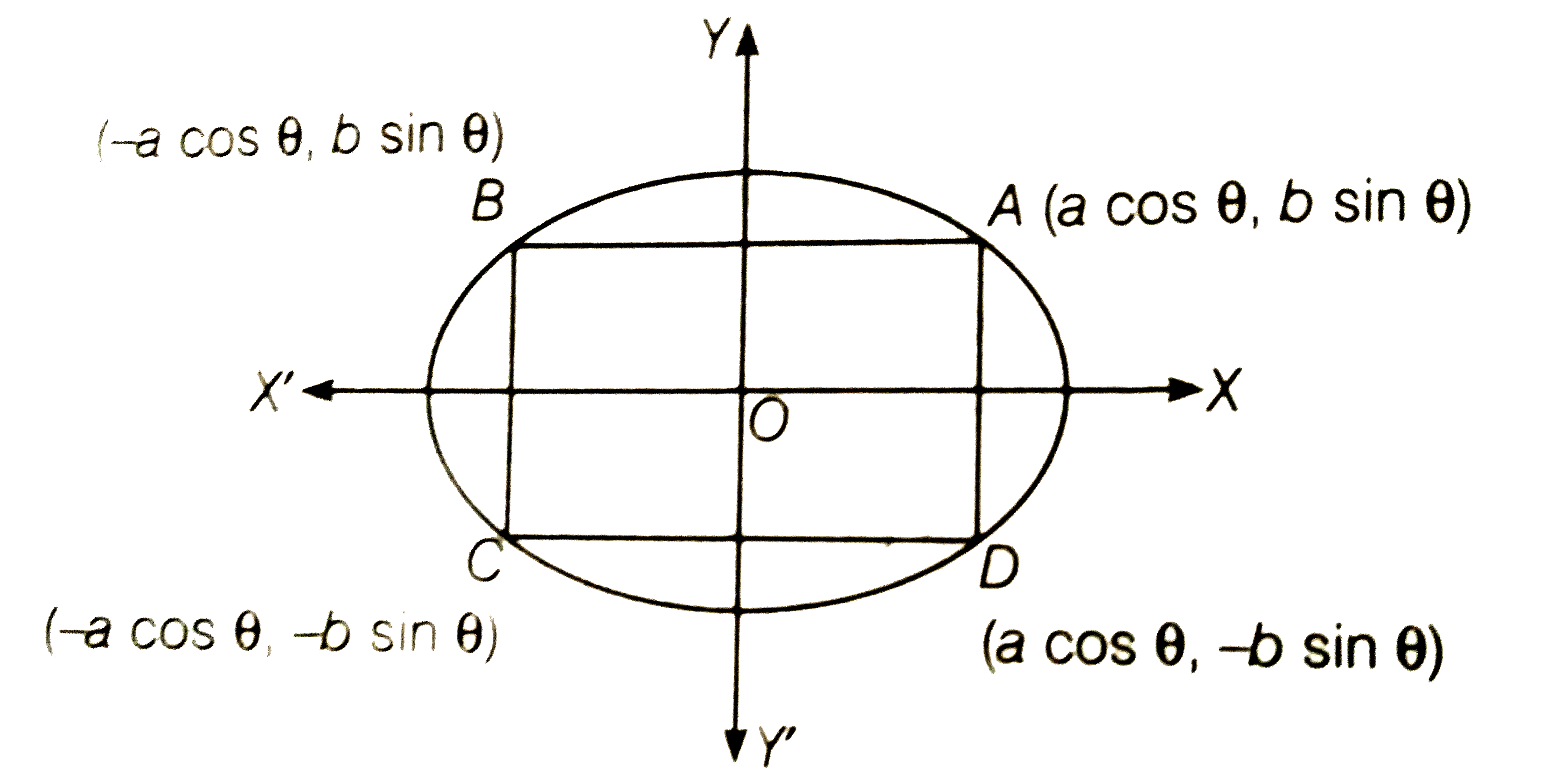
Let the coordinates of the vertices of rectangle ABCD are $A (a cos θ, b sin θ), B (- a cos θ, b sin θ)$ ,
$C (- a cos θ, - b sin θ)$ and $D (a cos θ, - b sin θ)$ , then length of rectangle $A B = 2 a cos θ$
and breadth of rectangle $A D = 2 b sin θ$
$∴$ Area of rectangle $= A B \times A D$
$= 2 a cos θ \times 2 b sin θ$
$\Rightarrow$ Area of rectangle $A = 2 a b sin 2 θ$
$∴ \frac{d A}{d θ} = 2 \times 2 a b cos 2 θ$
For maxima or minima put $\frac{d A}{d θ} = 0$
$\Rightarrow cos 2 θ = 0$
$\Rightarrow 2 θ = \frac{π}{2} \Rightarrow θ = \frac{π}{4}$

Now, $\frac{d^{2} A}{d θ^{2}} = - 8 a b sin 2 θ$
At $θ = π / 4, {(\frac{d^{2} a}{d θ^{2}})}_{θ = \frac{π}{4}} < 0$
$∴$ Area is maximum at $θ = \frac{π}{4}$
$\Rightarrow$ Maximum area of rectangle $= 2 a b$ sq units.
[ from Eq. (i) ]

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the area of the greatest rectangle that can be inscribed in an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
A $\sqrt{a b}$
B $a / b$
C $2 a b$
D $a b$
Question 2 - Select One
The sides of the greatest rectangle that can be inscribed in the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ are
A $a \sqrt{2}, b \sqrt{2}$
B $\sqrt{a}, \sqrt{b}$
Ca,b
D $\frac{a}{\sqrt{2}}, \frac{b}{\sqrt{2}}$
Question 3 - Select One
Consider an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
What is the area of the greatest rectangle that can be inscribed in the ellipse?
Aab
B2ab
Cab/2
D $\sqrt{a b}$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DERIVATIVES-MISCELLANEOUS PROBLEMS

Home
Ask Doubt
Profile