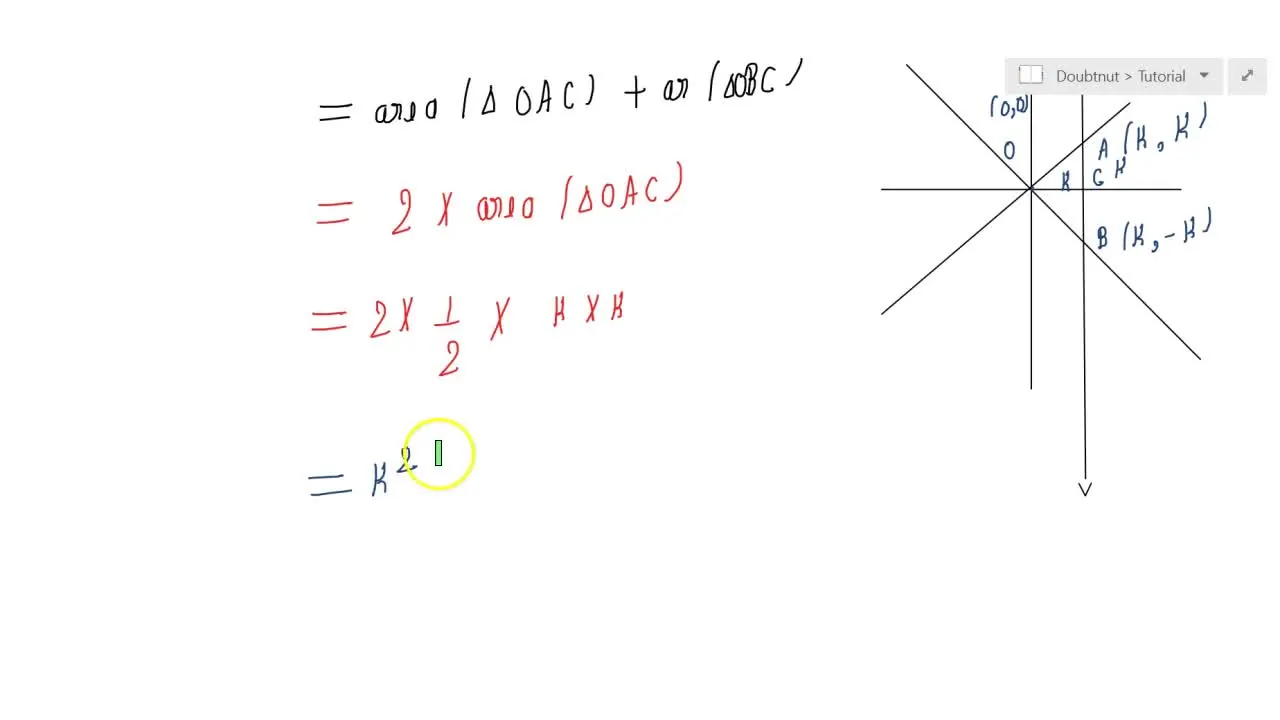Find the area of the triangle formed by the lines y−x=0,x+y=0and x−k=0.
Equation of line 1,L1→y−x=0⇒x=y→(1)
Equation of line 2,L2→x+y=0⇒x=−y→(2)
Equation of line 3,L3→x−k=0⇒x=k→(3)
Now, if we draw these lines, it will form a triangle with vertices, (0,0),(k,k),(k,−k).
Please refer to video for the diagram.
Now, from the diagram, we can see that,
Base of triangle =2k
Altitude of triangle =k
So, Area of triangle = 1/2*base*height
∴ Area =12⋅2k⋅k=k2 square units
Related Playlists
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.114videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.220videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.318videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.210videos
STATISTICS
- BOOK - NCERTCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE 3.17videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Find the area of the triangle formed theby lines y−x=0,x+y=0andx−k=0.
View SolutionFind the area of the triangle formed by the lines x=0, y=1 and 2x+y=2.
View SolutionFind the area of the triangle formed by the lines y=x,y=2x,y=3x+4
View SolutionFind the area of triangle formed by the lines : y=0, x=2 and x+2y=3.
View SolutionWhat is the area of the triangle formed by the lines y−x=0,y+x=0,x=c ?
View SolutionFind by integration, the area of the triangle bounded by the lines 4y-5x=0 and x=4.
View SolutionFind the area of triangle formed by the lines : x+y−6=0, x−3y−2=0 and 5x−3y+2=0
View SolutionFind the area of the triangle formed by the straight lines y=2x,x=0 and y=2 by integration.
View SolutionArea of triangle formed by straight lines x=0,x+2y=0andy=1
View SolutionFind the area of the triangle formed by the lines y2−9xy+18x2=0andy=9.
View Solution