Find the coordinates of one vertex of an equilateral triangle with centroid at the origin and the opposite side x+y−2=0.

A

(−1,−1)

B

(2,2)

C

(−2,−2)

D

(2,−2)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Let ABC be the equilateral triangle iwth vertex A(h,k).
Let the coordinates of D are (α,β).
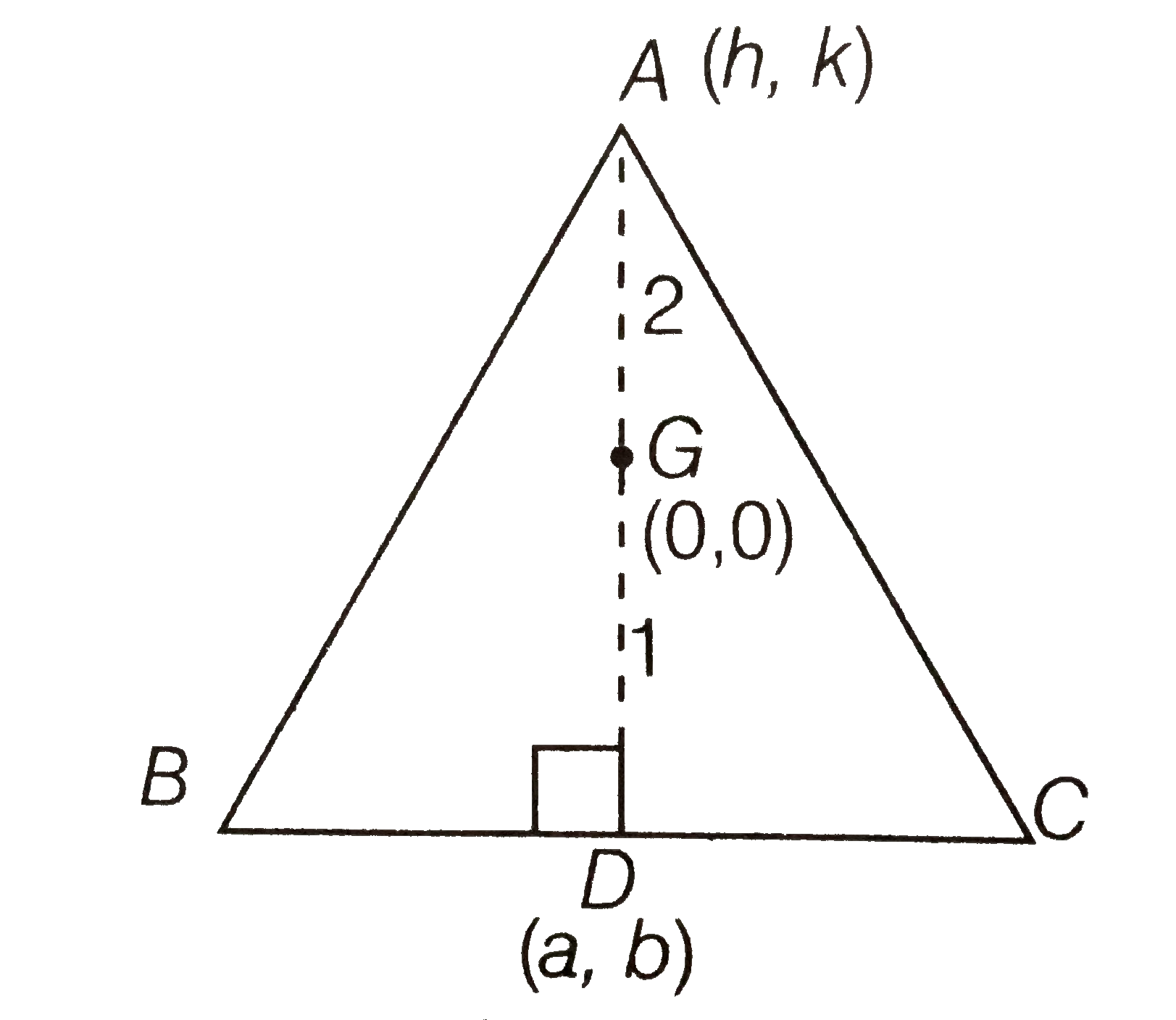
ocr_image
We know that 2:1 from the vertexA.
∴0=2α+h3 and 0=2β+k3
⇒2α=−h ......(i)
and 2β=−k
Also, D (α,β)lies on the line x+Y−2=0......(ii) .
∴α+β−2=0
AD⊥BC
Since, the slope of line BC i.e., mBC=−1
and slope of the line AG i.e., mAG=k−0h−0=kh
⇒(−1).(kh)=−1
⇒h=k ......(iii)
From Eqs. (i) and (iii),
2α=−h and 2β=−h
∴α=β
From Eq. (ii), 2α−2=0⇒α=1
If α=1 then β=1
So, the vertex A is (−2,−2).

Updated on:21/07/2023
|
Class 11MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions