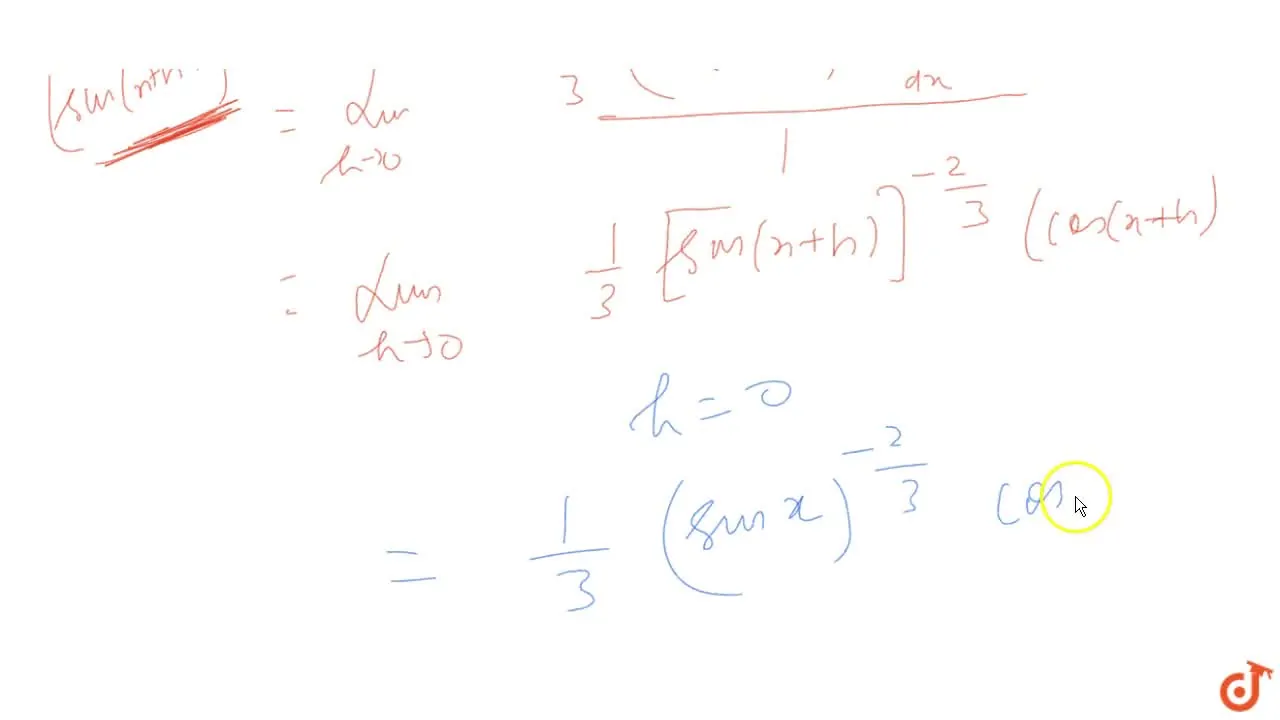Find the derivative of s∈x3 from first principles.
Video Solution
Text Solution
Herte, f(x)=3√sinx
∴f'(x)=Limh→0f(x+h)−f(x)h
=Limh→03√sin(x+h)−3√sinxh
As this is a 00form. So, we will apply L'hospital rule to evaluate this limit and differentiate it w.r.t. h.
=Limh→013(sin(x+h)−23(cos(x+h)))−01
=13(sinx)−23cosx
∴f'(x)=13(sinx)−23cosx
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Find the derivative of cos x from first principle.
View SolutionFind the derivative of cos x from first principle.
View SolutionFind the derivative of s∈x3 from first principles.
View SolutionFind the derivative of esinx from the first principle.
View SolutionFind the derivative of f (x) from the first principles, where f(x) is (i) sinx+cosx
View SolutionFind the derivative of f from the first principles, where f is given by(i) f(x)=2x+3x−2 (ii) f(x)=1x
View SolutionFind the derivative of √cosecx from first principle.
View SolutionFind the derivative of sinx using first principle
View SolutionFind the derivative of tan2x using first principle.
View SolutionFind the derivative of x−3/2 from the first principle .
View Solution