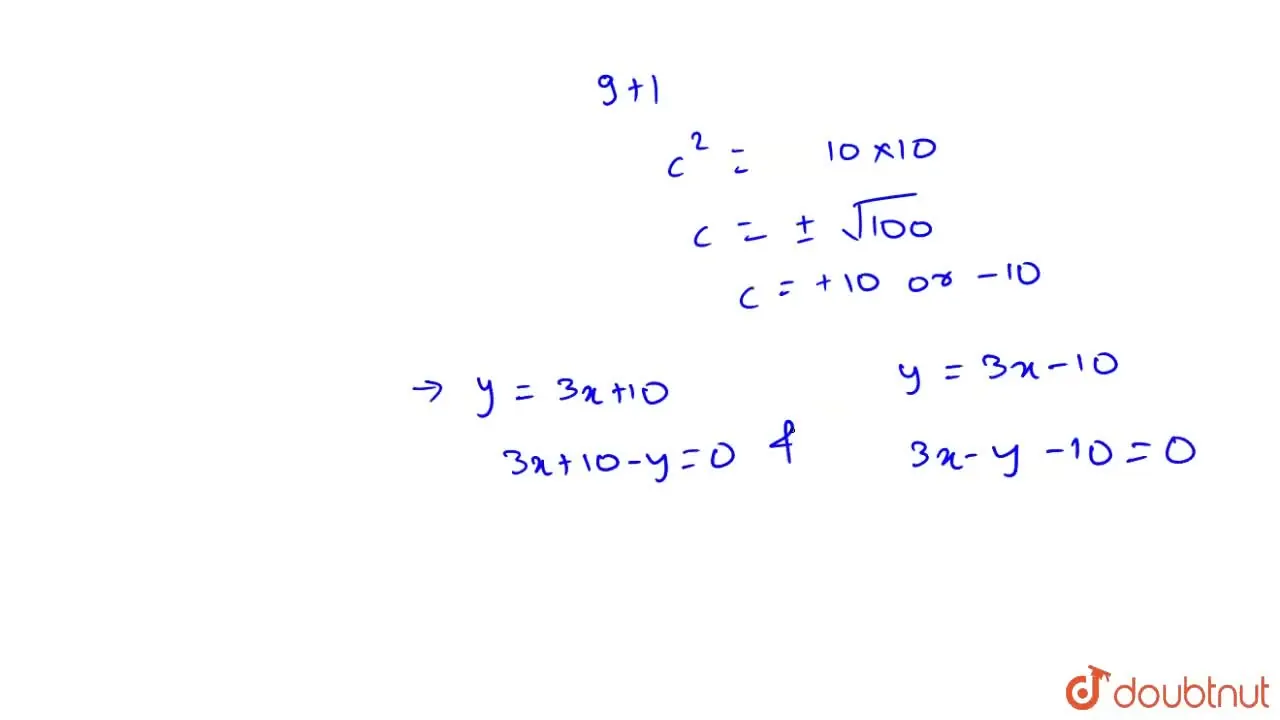Find the equation of a line with slope 3 and the length of the perpendicular from the origin equal to √10
Let c be the intercept on y-axis
Then, the equation of the line is
y=3x+c
⇒−33x+y=c
⇒−3√(−3)2+12x+y√(−3)2+12=c√(−3)2+12
⇒−3√10x+y√10=c√10
This is the normal form of the equation
Thus, c√10 denotes the length of perpendicular from the origin. But, the length of the perpendicular from the origin is √10
∴ The required lines are −3x+y=±10
or y=3x±10
∴∣∣∣c√10∣∣∣=√10
⇒|c|√10=√10
⇒|c|=1=±10.
∴ The required lies are −3x+y=±10ory=3x±10
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - TRY YOURSELF23videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTECHAPTER - STRAIGHT LINESEXERCISE - ASSIGNMENT (SECTION A) (OBJECTIVE TYPE QUESTIONS) (ONLY ONE ANSWER)50videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTECHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason15videos
STATISTICS
- BOOK - AAKASH INSTITUTECHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J10videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Find the equation of a line with slope 2 and the length of the perpendicular form the origin equal to √5 .
View SolutionFind the equation of a line with slope −1 and whose perpendicular distance from the origin is equal to 5
View SolutionFind the equation of a line with slope –1 and whose perpendicular distance from the origin is equal to 5.
View SolutionFind the length of the perpendicular from the origin to the line 4x+3y-2=0
View SolutionFind the equation of the straight line upon which the length of the perpendicular from the origin is 5and the slope of this perpendicular is 34.
View SolutionFind the equation of the straight line upon which the length of the perpendicular from the origin is 2 and the slope of this perpendicular is 512.
View SolutionFind the equation of the straight line on which the length of the perpendicular from the origin is 2 and the perpendicular makes an angle α with x-axis such that sinα=13.
View SolutionFind the equation of the straight line on which the length of the perpendicular from the origin is 4 units and the line makes an angle of 1200 with positive direction of x−aξs.
View SolutionFind the equation of the line on which the length of the perpendicular segment from the origin to the line is 4 and the inclination of the perpendicular segment with the positive direction of x-axis is 300.
View SolutionFind the equation of the line on which length of the perpendcular from the origin is 5 and the angle which this perpendicular makes with the x-axis is 60∘ ,
View Solution