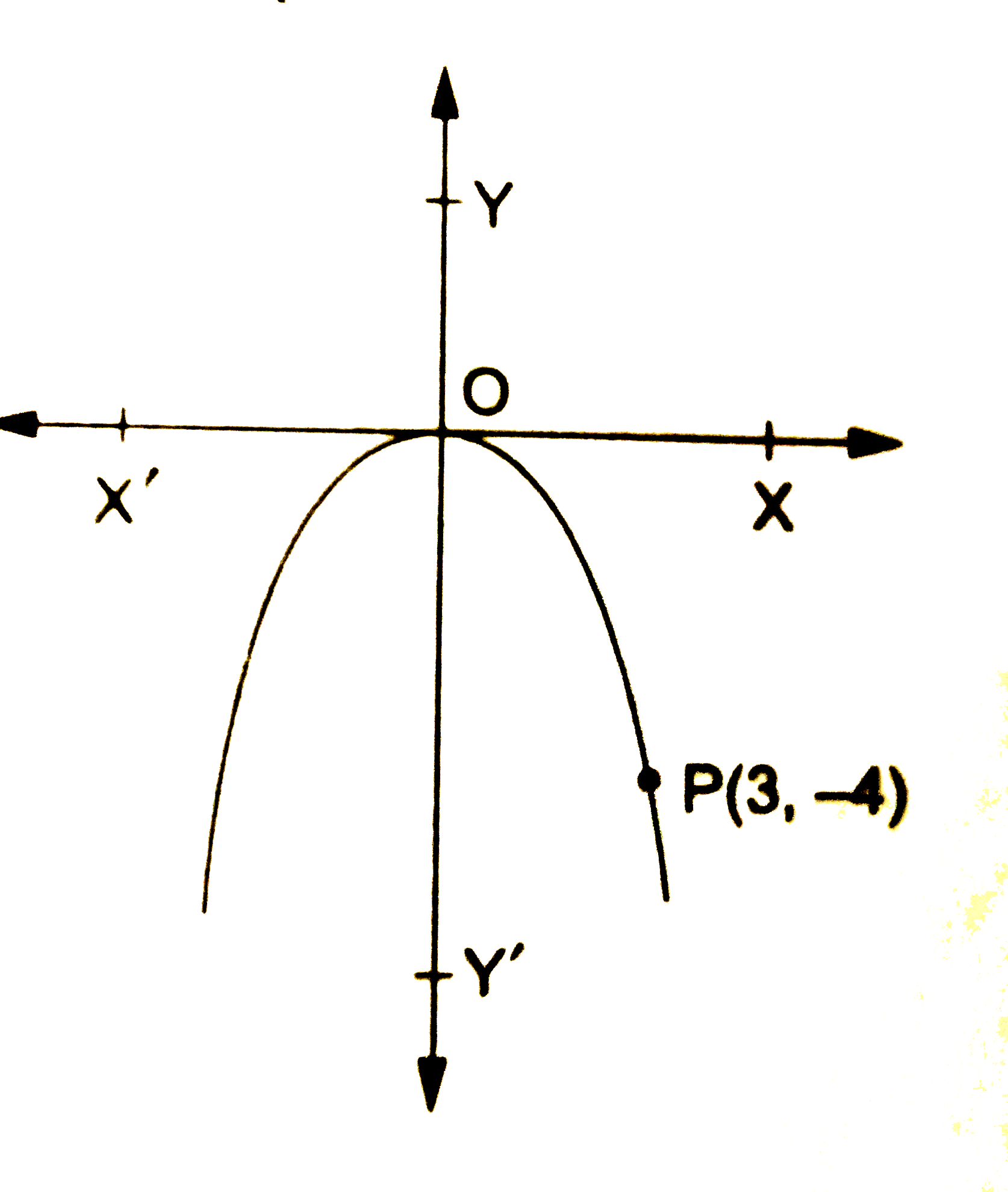
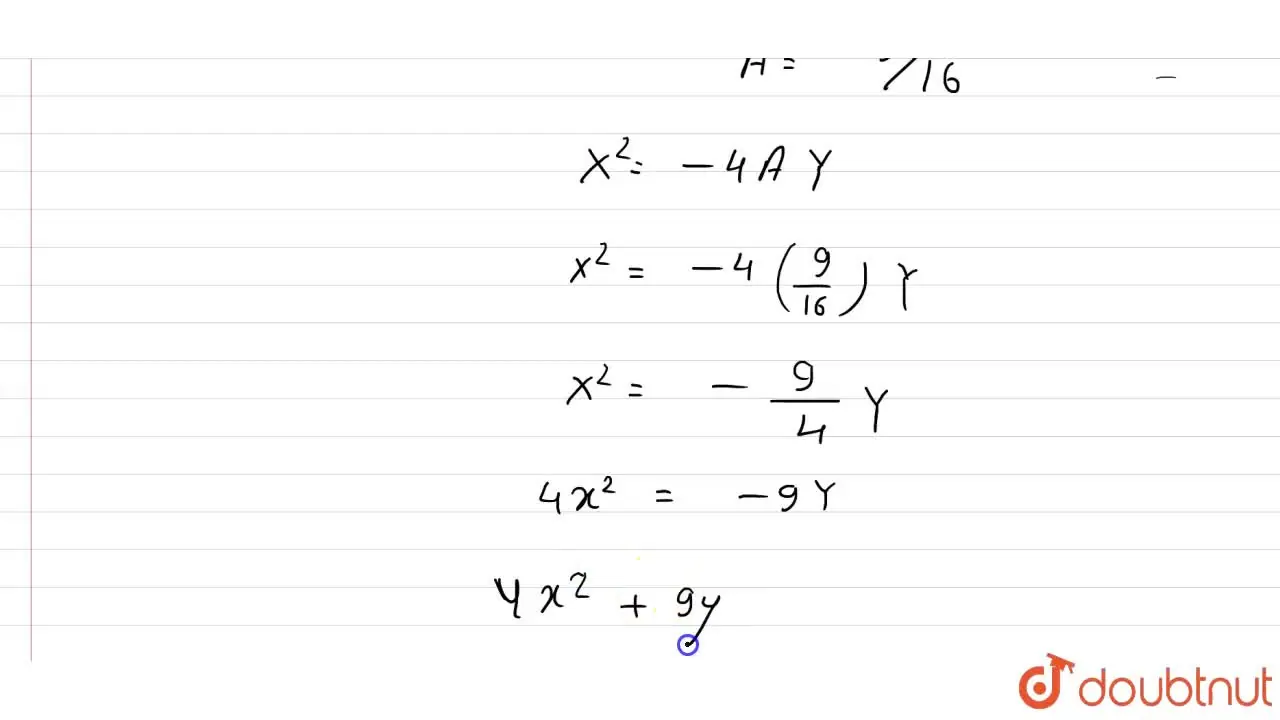Find the equation of the parabola with vertex at the origin, passing throgh the point P(3,-4) and symmetric about the y-axis.
It is given that the vertex of the parabola is O(0,0) and it is symmetric about the y-axis, So, its equation is . Since the parabola passes through the point so it lies in the 4th quadrant.
it is downward parabola. Let the equation be . Since it passes through the point P(3,-4) we have
So, the required equation is
Related Playlists
Similar Questions
Find the equation of the parabola with vertex at the origin, passing through the point P(5,2) and symetric with respect to the y-axis.
View SolutionFind the equation of the parabola with vertex at the origin and focus F(0,5).
View SolutionFind the equation of the parabola with vertex at the origin and focus at F(-2, 0).
View SolutionFind the equation of a parabola with vertex at the origin and the directrix, y=2.
View SolutionFind the equation of the parabola with vertex at origin and focus at (−3,0) .
View SolutionFind the equation of the parabola with vertex at origin and focus at (0,−7).
View SolutionThe equation of the parabola with vertex at the origin passing through (2,3) and the axis along x-axis is
View SolutionFind the equation of the parabola whose vertex is at the origin and directrix is the line y−4=0
View SolutionFind the equation of the parabola which is symmetric about the y-axis and passes through the point (2,−4).
View SolutionFind the equation of the parabola which is symmetric about the x-axis and passes through the point (−2,−3)
View Solution