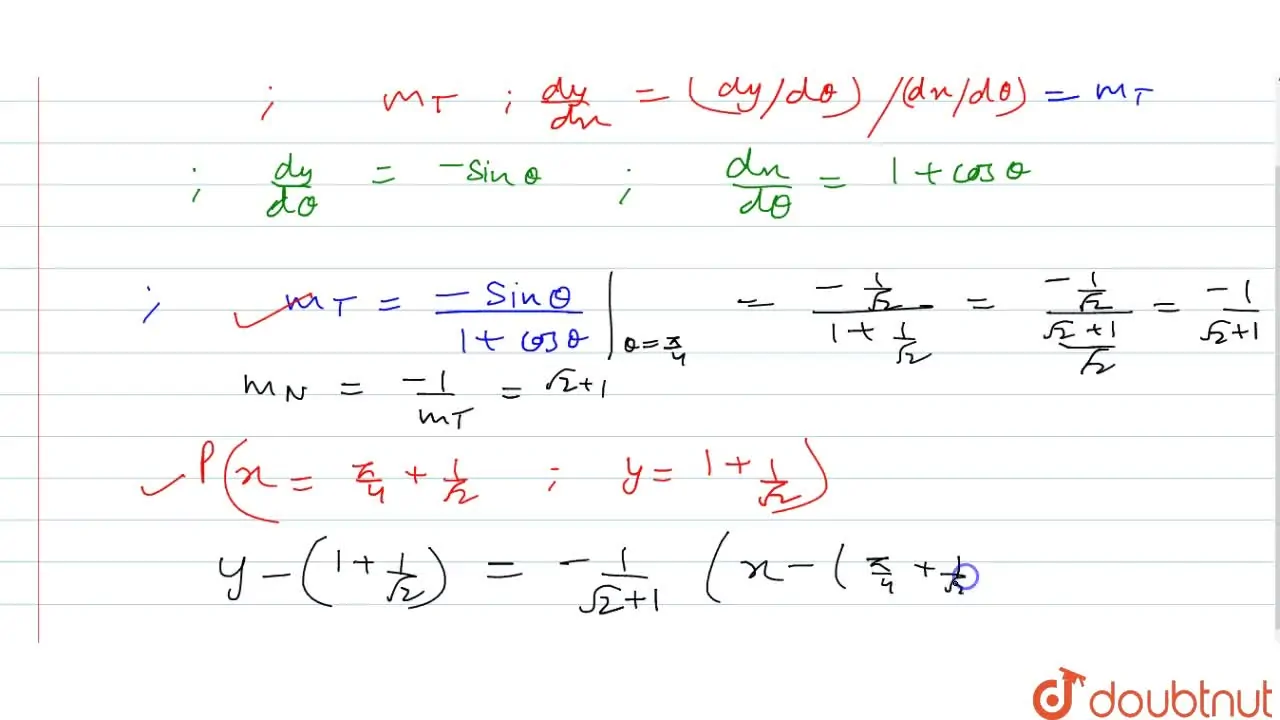Find the equation of the tangent to the curve x=θ+sinθ , y=1+cosθ at θ=π/4 .
To find equation of the tangent, we need slope and one point on the tangent. point on the tangent at θ=π4
$$
x=\frac{\pi}{4}+\sin \left(\frac{\pi}{4}\right)=\frac{\pi}{4}+\frac{1}{\sqrt{2}}
$$
and
$$
\mathrm{y}=1+\cos \left(\frac{\pi}{4}\right)=1+\frac{1}{\sqrt{2}}
$$
Therefore point P(π4+1√2,1+1√2) lies on the line.
To find the slope, we find dydx
$$
\frac{\mathrm{dx}}{\mathrm{d} \theta}=1+\cos \theta
$$
and
$$
\frac{d y}{d \theta}=-\sin \theta
$$
Thus,
$$
\frac{d y}{d x}=\frac{-\sin \theta}{1+\cos \theta}
$$
Solving above,
$$
\frac{d y}{d x}=\frac{-2 \cdot \sin \frac{\theta}{2} \cos \frac{\theta}{2}}{2 \cdot \cos ^{2} \frac{\theta}{2}}
$$
$$
\frac{d y}{d x}=-\tan \frac{\theta}{2}
$$
Thus
$$
\frac{\mathrm{dy}}{\mathrm{dx}}=-\tan \left(\frac{\pi}{8}\right) \text { at } \theta=\frac{\pi}{4}
$$
slope
$$
\mathrm{m}=-\tan \left(\frac{\pi}{8}\right)=(1-\sqrt{2})
$$
Now apply point slope form to get equation of tangent,
$$
\begin{aligned}
&{\left[y-\left(1+\frac{1}{\sqrt{2}}\right)\right]=(1-\sqrt{2})\left(x-\frac{\pi}{4}-\frac{1}{\sqrt{2}}\right)} \\
&(\sqrt{2}-1) x+y-1-\frac{1}{\sqrt{2}}+\left(\frac{\pi}{4}+\frac{1}{\sqrt{2}}\right)(1-\sqrt{2})=0
\end{aligned}
$$
or
$$
(\sqrt{2}-1) x+y-1-\frac{1}{\sqrt{2}}+\left(\frac{\pi}{4}\right)(1-\sqrt{2})+\frac{1}{\sqrt{2}}(1-\sqrt{2})=0
$$
Simplifying we get,
$$
(\sqrt{2}-1) x+y+\left(\frac{\pi}{4}\right)(1-\sqrt{2})-2=0
$$
Related Playlists
Similar Questions
Find the equation of the tangent to the curve x=θ+sinθ,y=1+cosθ, at θ=π4
View SolutionFind the equations of the tangent and the normal to the curve x=θ+sinθ , y=1+cosθ at θ=π/2 at indicated points.
View SolutionFind the equation of tangent to the curve x=a(θ+sinθ),y=a(1−cosθ) at a point θ
View SolutionFind the equation of the tangent line to the curve x=1−cosθ, y=θ−sinθ at θ=π/4 .
View SolutionThe equation of tangent to the curve x=a(θ+sinθ),y=a(1+cosθ) at θ=π2 is
View SolutionFind the equations of the tangent and normal to the curve x=asin3θandy=acos3θ at θ=π4.
View SolutionFind the equations of the tangent and the normal to the curve x=a(θ+sinθ), y=a(1−cosθ) at θ at indicated points.
View SolutionThe equation of tangent to the curve x=sinθandy=cos2θ at θ=π6 is
View SolutionFind the equations of tangent to the curve x=1−cosθ,y=θ−sinθ at θ=π4
View SolutionThe equation of tangent to the curve x=acos3θ,y=asin3θ at θ=π4 is
View Solution