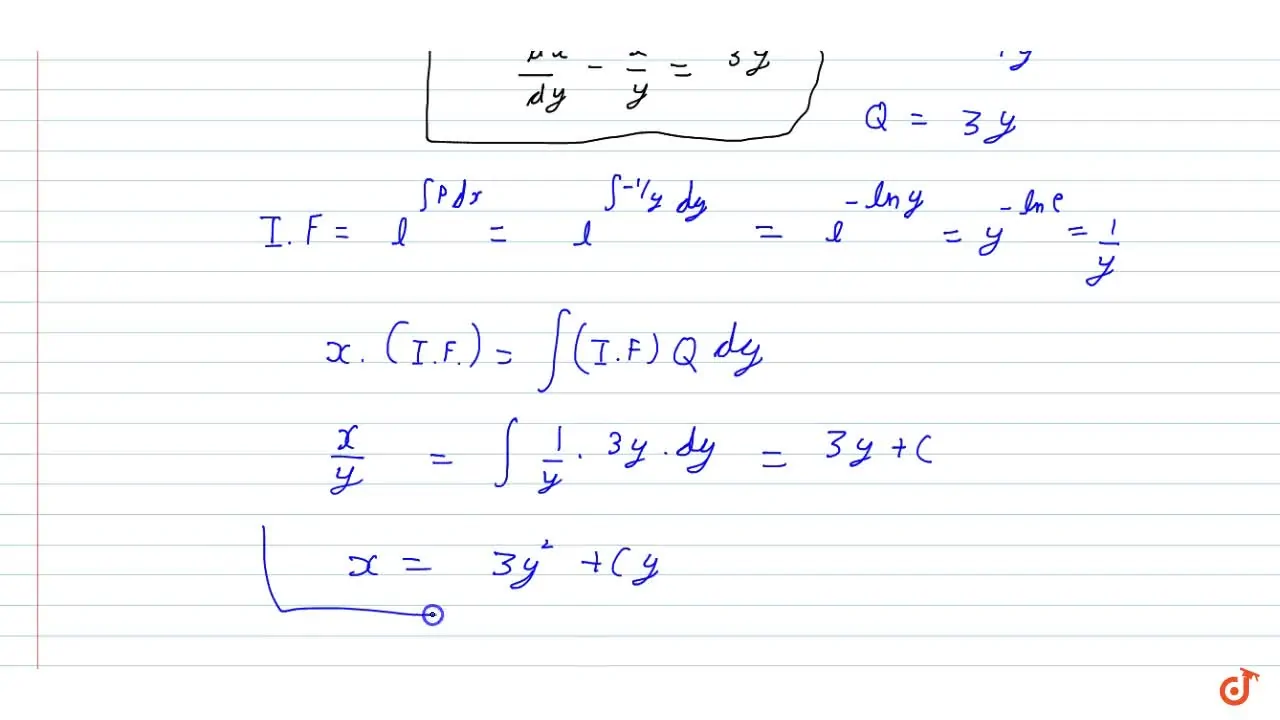Find the general solution of the differential equations:(x+3y2)dxdy=y(y>0)
Video Solution
Text Solution
Here, given equation is,
(x+3y2)dydx=y
⇒dxdy=x+3y2y
⇒dxdy−xy=3y
Comparing it with dxdy+Px=Q
P=−1yandQ=3y
Integrating factor, I.F.=e∫Pdy
I.F.=e∫−1ydy=e−lny=y−lne=y−1=1y
Now, general solution will be,
x(I.F.)=∫(I.F.)Qdy
⇒xy=∫(1y)(3y)dy
⇒xy=3y+c
⇒x=3y2+cy
|
Updated on:21/07/2023
Similar Questions
Find the general solution of the differential equations:(x+y)dxdy=1
View SolutionFind the general solution of the differential equations:dxdy+3y=e−2x
View SolutionFind the general solution of the differential equation (x+2y3)dydx=y,y≠0
View SolutionFind the general solution of the differential equation dydx−y=cosx
View SolutionFind the general solution of the differential equations:xdxdy+2y=x2logx
View SolutionFind the general solution of the differential equations:dxdy+yx=x2
View SolutionFind the general solution of the differential equations:xlogxdxdy+y=2xlogx
View SolutionThe general solution of the differential equation dydx=yx is
View SolutionThe general solution of the differential equation
dydx=ex+y isView SolutionFind the general solution of the differential equations y log y dx – x dy = 0
View Solution