Find the intervals in which the following functions are strictly increasing or decreasing: (a x2+2x−5 (b) 10−6x−2x2 (c) −2x3−9x2−12x+1 (d) 6−9x−x2 (e) (x+1)3(x−3)3
(a) f(x)=x2+2x+5
f'(x)=2x+2
Letf'(x)=0

⇒2x+2=0
⇒x=−1

∴F(x) is strictly decreasing in (−∞,−1) and strictly increasing in (=1,∞).
(b) f(x)=10−6x−2x2
⇒f'(x)=−6−4x
Let f'(x)=0
⇒−6−4x=0
⇒x=−32
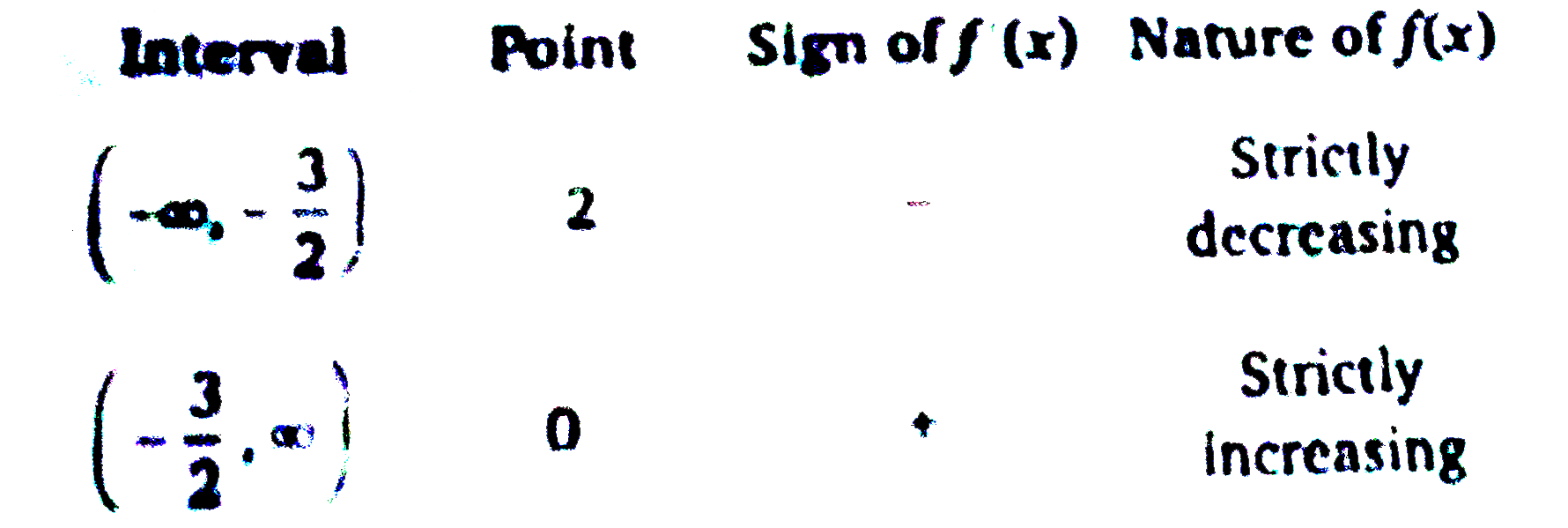
∴f(x) is strictly decreasing in (−∞,−32) and strictly increasing in (−32,∞).
(c) f(x)=−2x3−9x2−12x−1
⇒f'(x)=−6x2−18x−12
=−6(x2+3x+2)
=−6(x+1)(x+2)
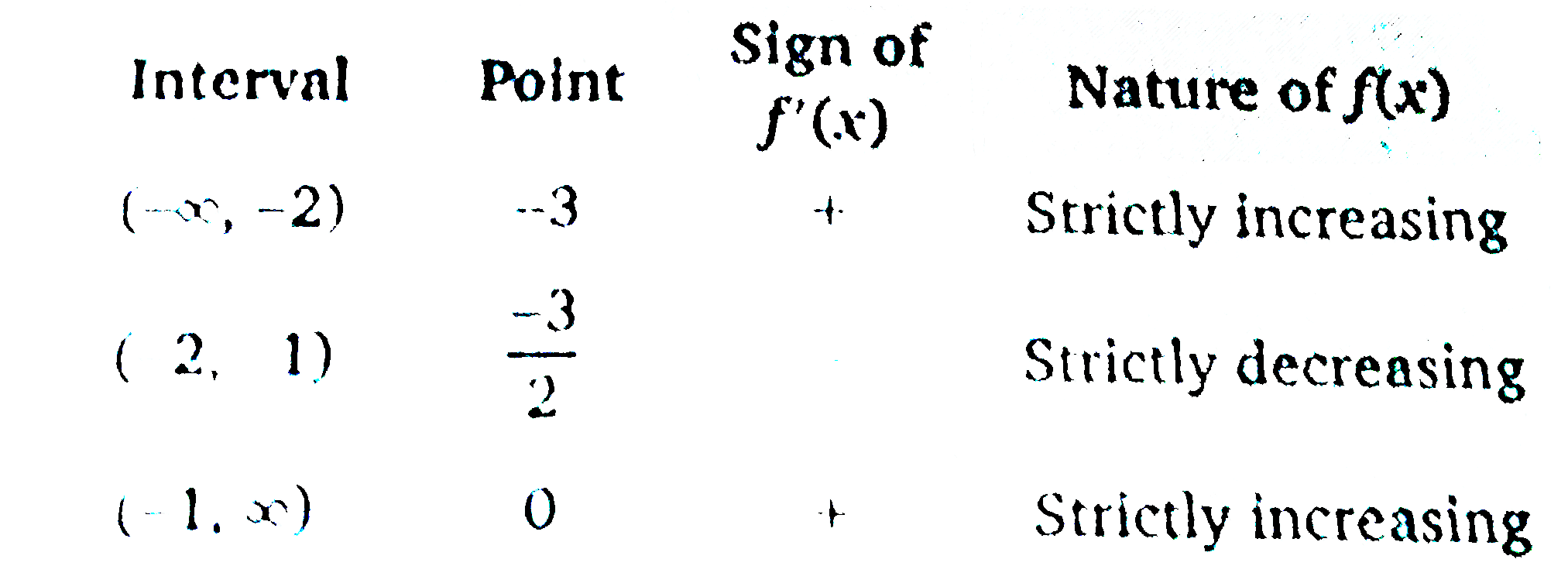
Let f'(x)=0
⇒−6(x+1)(x+2)=0
⇒x+1=0orx+2=0
⇒x=−1orx=−2

∴f(x) is strictly decreasing in (−2,−1) and atrictly increasing in (−∞,−2)∪(−1,∞).
(d) f(x)=6−9x−x2
Let f'(x)=0
⇒−9−2x=0
⇒x=−92
∴f(x),is strictly decreasing in (−∞,−92) and strictly increasing in(−92,∞).
(e) f(x)=(x+1)3(x−3)3
⇒f'(x)=(x+1)3⋅3(x−3)2+(x−3)3⋅3(x+1)2
=3(x+1)2(x−3)2(x+1+x−3)
=6(x+1)2(x−3)2(x−1)
If f'(x)>0
then 6(x+1)2(x−3)2(x−1)>0,x≠−1,x≠3
⇒x−1>0
⇒x>1
∴f(x) is strictly increasing in the interval (1,∞)−{3}.
Again f'(x)<0
⇒3(x+1)2(x−3)2)(x−1)<0x≠−1,x≠3
⇒x−1<0
⇒x<1
∴f(x) is strictly decreasing in the interval (−∞,1)−{−1}.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.327videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.49videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 6.118videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHANCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
Similar Questions
Find the invervals in which the following functions are strictly increasing or decreasing :
6−9x−x2View SolutionFind the invervals in which the following functions are strictly increasing or decreasing :
−2x3−9x2−12x+1View SolutionFind the intervals in which the given function is strictly increasing : −2x3−9x2−12x+1
View SolutionFind the intervals in which the following functions are strictly increasing or decreasing:(a) x2+2x−5 (b) 10−6x−2x2 (c) −2x3−9x2−12x+1 (d) 6−9x−x2(e) (x+1)3(x−3)3
View SolutionFind the interval in which the following function are strictly increasing or decreasing ? A. x2+2x+5 B. 10−6x−2x2
View SolutionDetermine the intervals in which the following functions are strictly increasing or strictly decreasing :
f(x)=x2+2x−5View SolutionDetermine the intervals in which the following functions are strictly increasing or strictly decreasing :
f(x)=6−9x−2x2View SolutionDetermine the intervals in which the following functions are strictly increasing or strictly decreasing :
f(x)=x8+6x2.View SolutionDetermine the intervals in which the following functions are strictly increasing or strictly decreasing :
f(x)=x3−6x2+9x+8View SolutionDetermine the intervals in which the following functions are strictly increasing or strictly decreasing :
f(x)=20−9x+6x2−x3View Solution

