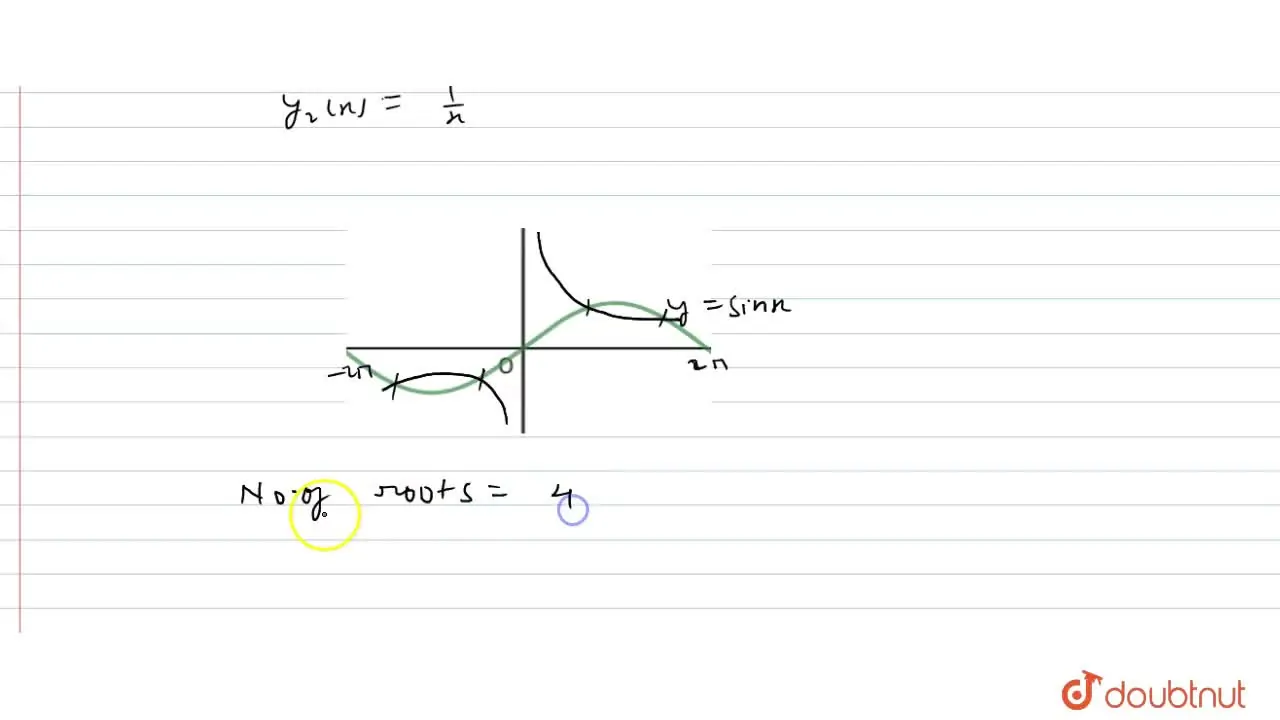
Find the number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π].
We have x sin x = 1
∴ sinx=1x
Number of roots of the above equation = number of points (s) of the intersection of the graphs of y=sinx and y=1x for x∈[−2π,0)∪(0,2π]
The graphs of both functions are as shown in the following figure.
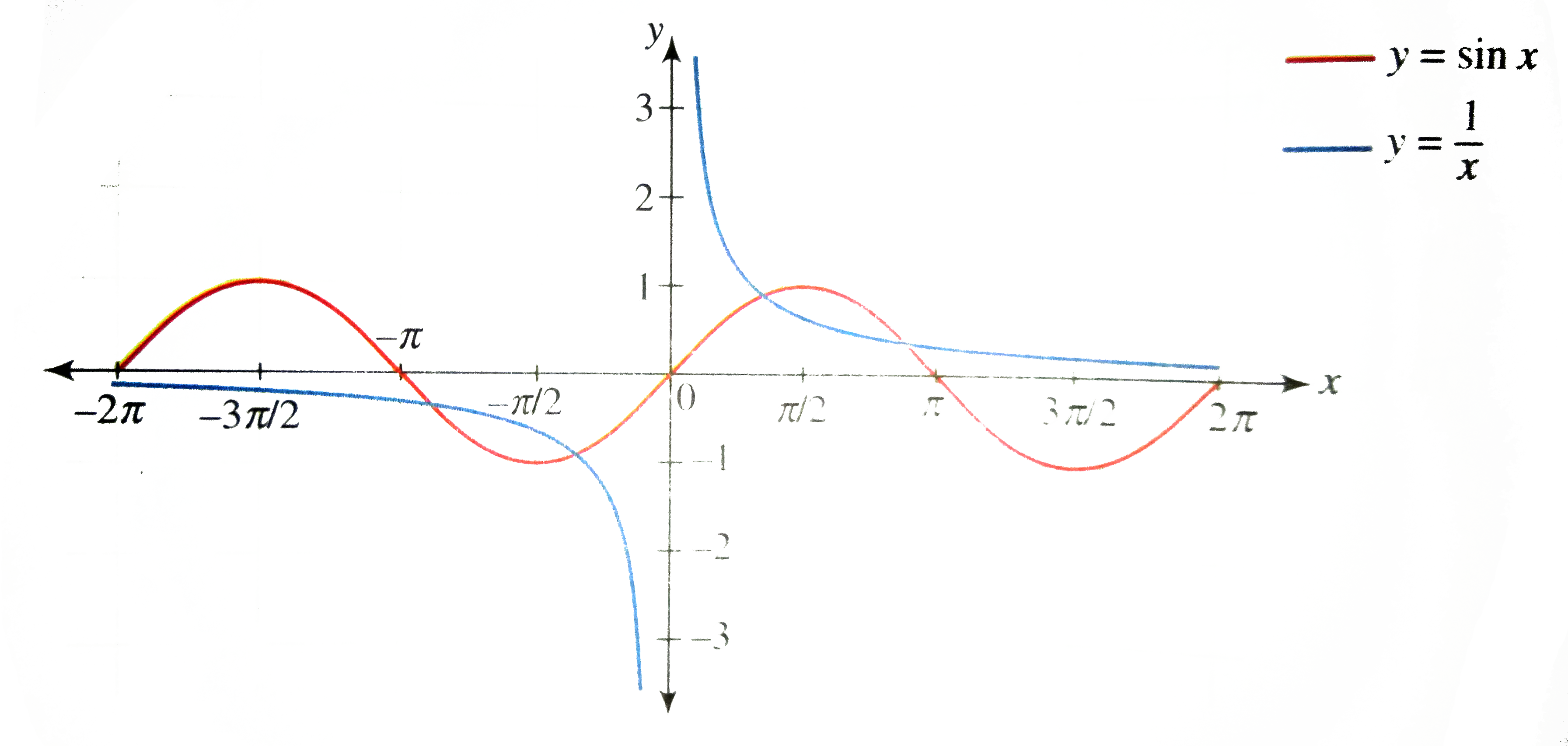
Graphs intersect at four points, hence four roots.
Related Playlists
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
Similar Questions
The number of roots of the equation xsinx=1,,x∈[−2π,0]∪(0,2π) is
View SolutionThe number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is 2 (b) 3 (c) 4 (d) 0
View SolutionThe number of real roots of the equation
x2+x+3+2sinx=0,x∈[−π,π], isView SolutionFind the number of solution of the equations
2cosx=|sinx|, when x∈[−2π,2π]View SolutionThe number of roots of the equation x3+x2+2x+sinx=0 in (−2π,2π)
View SolutionFind the number of roots of the equation tan(x+π6)=2tanx,forx∈(0,3π).
View SolutionFind the number of solution of the equation √cos2x+2=(sinx+cosx) in [0,π].
View SolutionFind the number of solution of the equations
x+2tanx=π2, when x∈[0,2π]View SolutionThe number of solutionsof the equation
1+sinxsin2x2=0 in [−π,π] isView SolutionThe number of solutions of the equation sinx.Sin2x.Sin3x=1 in [0,2π] is
View Solution