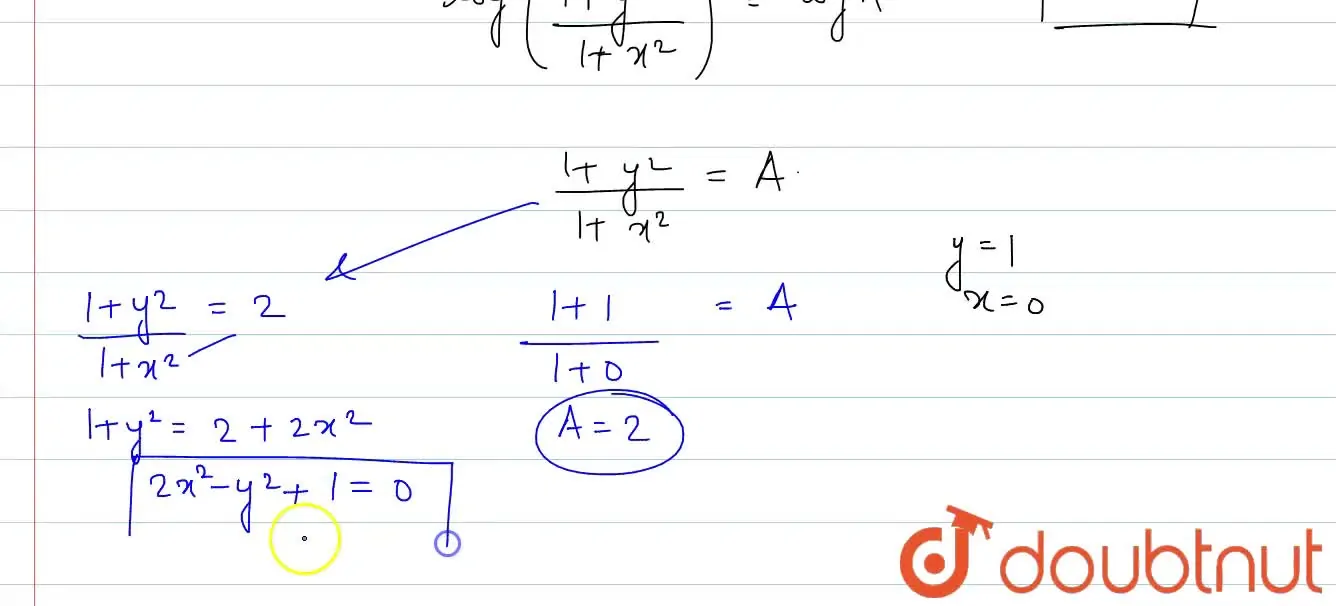
Find the particular solution of the differential equation x(1+y2)dx−y(1+x2)dy=0, given that y = 1 when x = 0.
The correct Answer is:y=√2x2+1
12∫2x(1+x2)dx−12∫2y(1+y2)dy=log|C1|
⇒12log(1+x2)−12log(1+y2)=log|C1|
⇒log(1+x2)−log(1+y2)=log∣∣C21∣∣=logC⇒(1+x2)(1+y2)=C. ...(i)
Putting x = 0 and y = 1 in (i) we get C = 12.
∴(1+y2)=2(1+x2)⇒y=√2x2+1.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS WITH VARIABLE SEPARABLEEXERCISE - Exercise 19A16videos
DIFFERENTIAL EQUATIONS WITH VARIABLE SEPARABLE
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS AND THEIR FORMATION EXERCISE - Exercise 18C16videos
DIFFERENTIAL EQUATIONS AND THEIR FORMATION
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIATIONEXERCISE - Exercise 10I51videos
DIFFERENTIATION
Similar Questions
Solve the differential equation x(1+y2)dx−y(1+x2)dy=0, given that y=0, when
View SolutionFind the particular solution of the differential equation (1+e2x)dy+(1+y2)exdx=0, given that y=1 when x=0.
View SolutionFind the particular solution of the differential equation ex√1−y2dx+yxdy=0, given that y=1 when x=0
View SolutionSolve the differential eqautionx(1+y2)dx−y(1+x2)dy=0, given that y=0 when x=1
View SolutionFind the particular solution of the differential equation: (1+e2x)dy+(1+y2)exdx=0, given that y=1, when x=0.
View SolutionFind the particular solution of the differential equation (1−y2)(1+logx)dx+2xydy=0, given that y=0 when x=1.
View SolutionFind the particular solution of the differential equation (1−y2)(1+logx)dx+2xydy=0 given that y=0 when x=1
View SolutionFind the particular solution of the differential equation ; (x2+xy)dy=(x2+y2)dx given that y=0 when x=1.
View SolutionFind the particular solution of the differential equation xdydx−y=(x+1)e−x given that y=0 when x=1.
View SolutionFind the particular solution of the differential equation x(x2−1)dydx=1, it being given that y=0 when x=2.
View Solution