Find the point (α,)β on the ellipse 4x2+3y2=12, in the first quadrant, so that the area enclosed by the lines y=x,y=β,x=α , and the x-axis is maximum.Solution in Tamil
The correct Answer is:(3/2,1)
The equation of the ellipse is x23+y24=1
Let point P be (√3cos,θ,2sinθ),θ∈(0,π/2)
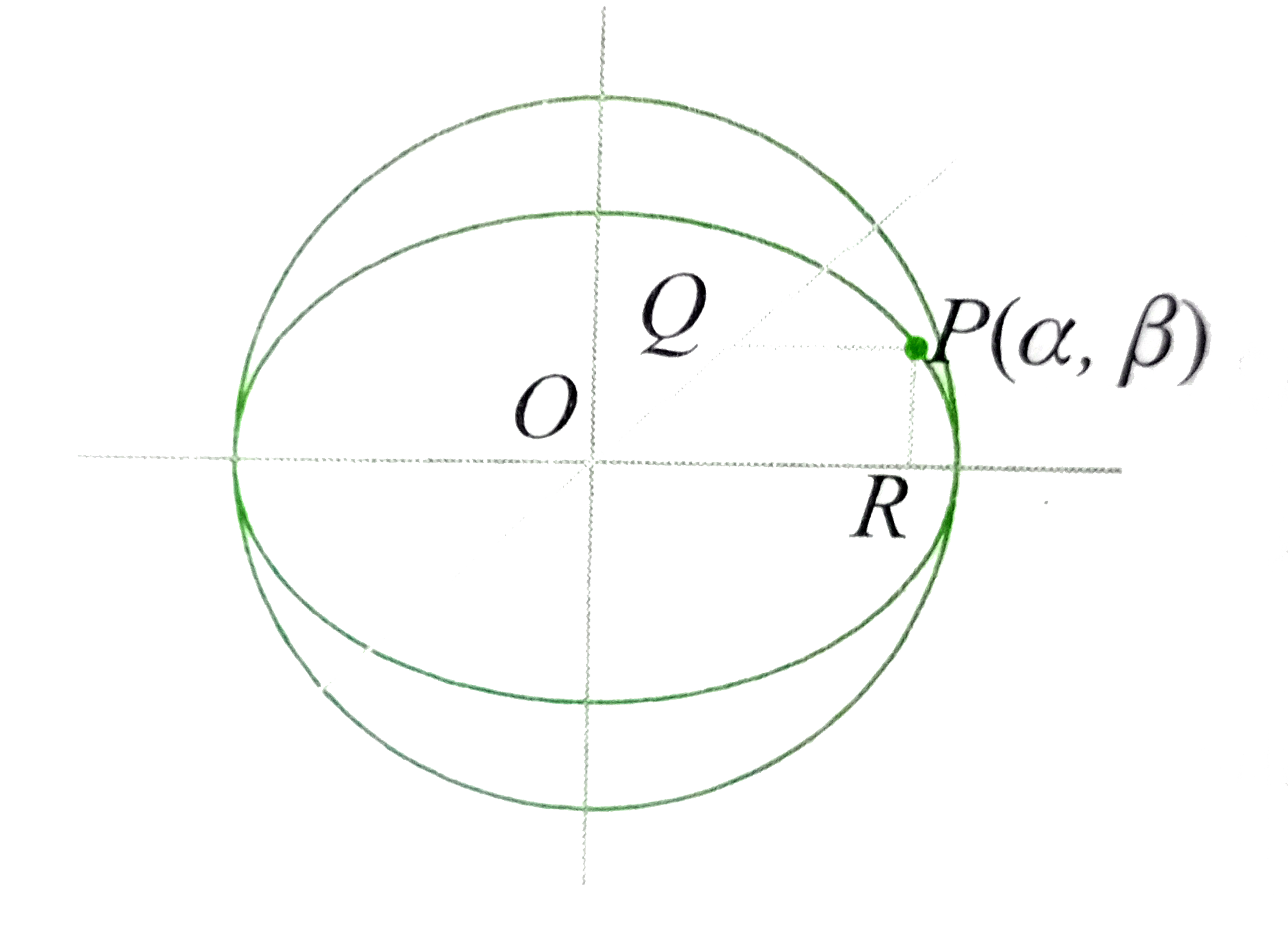
Clearly, line PQ is y=sinθ , line PR is x=√3cosθ, line OQ is y=x, and Q is (2sinθ,2sinθ),
Z= Area of region PQORP (tranpezium)
=12(OR+PQ)PR
=12(√3cosθ+√3cosθ−2sinθ)2sinθ
=(2√3cosθsinθ−2sin2θ)
=(√3sin2θ+cos2θ−1)
=2cosθ(2θ−π3)−1
which is maximum when cos(θ−π3) is maximum
∴2θ−π3=0
or θ=π6
Hence, point P is (3/2,1)
Similar Questions
agreed g(x) = cosx^(2),f(x) = sqrt(x) And alpha , beta (alpha lt beta) Quadratic equation 18x^(2)-9pix + pi^2 =0 Are the origin of. So curve y= (gof)(x) And lines x = alpha , x = beta And the area of the area enclosed by y = 0 (in square units) is
View Solutionfind the area of the region in the first quadrant enclosed by the X -axis , the line y=x and the circle x2+y2=32
View SolutionFind the area in the first quadrant enclosed by the X-axis,
the arc of the circle x2+y2=9 and the line 4x−3y=0.
View SolutionFind the area bounded by
xy=a2,y=0,x=α,x=β(β>α>0)
View SolutionFind the area enclosed by
xy=a2,x=0,y=α,y=β(β>α>0)
View Solutionthe lines x+y+1=0;4x+3y+4=0 and x+αy+β=0, where α2+β2=2, are concurrent
View SolutionIf (α,β) is a point on parabola y2=4x which is nearest to the circle x2+(y−12)2=1, then (α+β) is equal to
View SolutionFind the area bounded by
xy=a2,y=0,x=α,x=β(β>α>0)
View Solution
