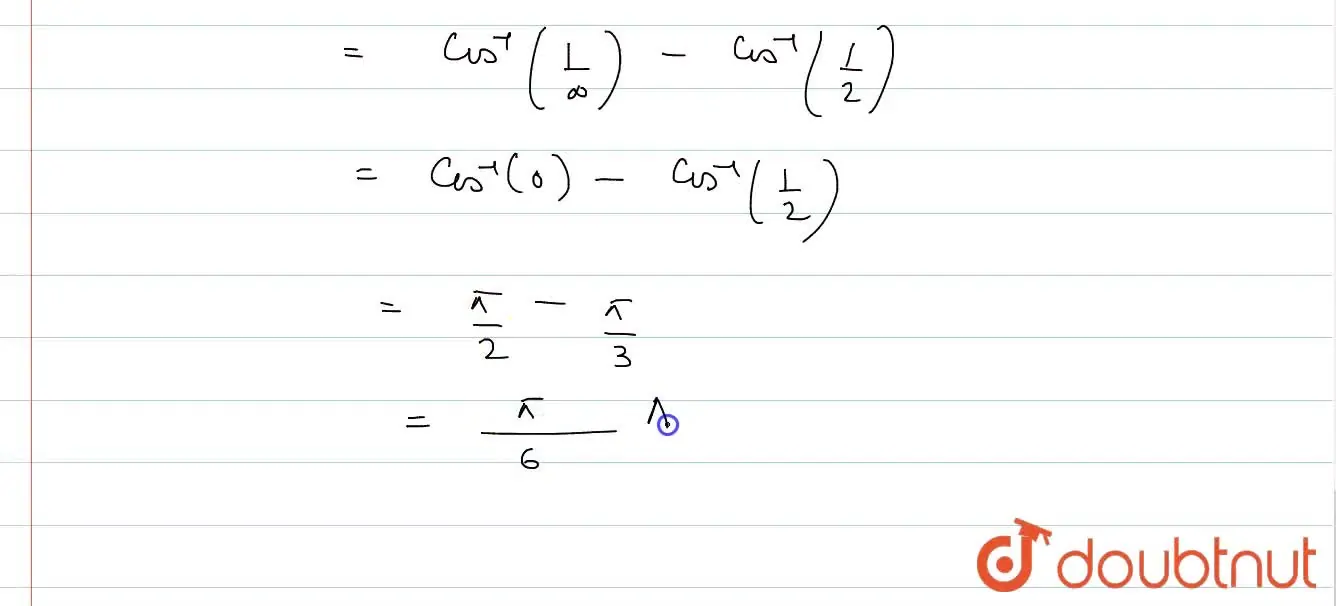Find the value
Video Solution
Text Solution
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank24videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - JEE Advanced Previous Year8videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year20videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
Find the value
limn→∞n∑k=2cos−1(1+√(k−1)k(k+1)(k+2)k(k+1))View SolutionUse Sandwich theorem to evaluate :Limn→∞(n+1)2∑k=n21√k
View SolutionFind the value of limn→∞n∑k=1(kn2+k).
View SolutionThe value of cot[100Σn=1cot−1(1+nΣk=12k)] is
View SolutionFind the value of limn→∞n∑k=1k2+k−1(k+1)!.
View Solutionn∑k=1k(1+1n)k−1 =
View SolutionFind the value of 3∞∑n=1⎧⎪⎨⎪⎩1π∞∑k=1cot−1⎛⎜⎝1+2 ⎷k∑r=1r3⎞⎟⎠⎫⎪⎬⎪⎭n
View Solutionn∑k=1(2k+3k−1)
View SolutionIf n∑k=0(k2+k+1)k!=(2007).2007!, then value of n is
View SolutionEvaluate : limn→∞1n2n−1∑k=0[k∫k+1k√(x−k)(k+1−x)dx]
View Solution