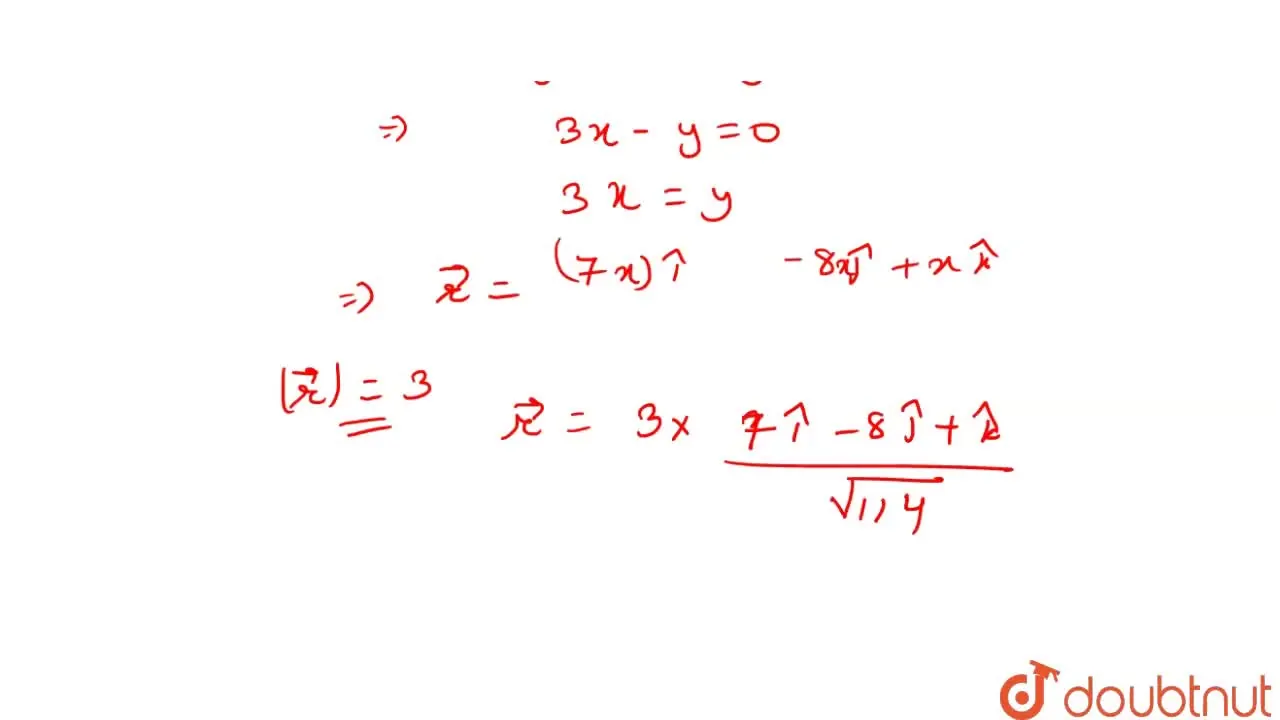Find the vector of length 3 unit which is perpendicular to ˆi+ˆj+ˆk and lies in the plane of ˆi+ˆj+ˆkand2ˆi−3ˆj
Given vectors are
→a=ˆi+ˆj+ˆk
→b=ˆi+ˆj+ˆk
→c=2ˆi−3ˆj
vector perpendicular to vectors →band→cis→b×→c.
vector perpendicular to →aand→b×→cis→a×(→b×→c) which lies in the pllane of →band→c. therefore
→a×(→b×→c)=[(ˆi+ˆj+ˆk)×{(ˆi+ˆj+ˆk)×(2ˆi−3ˆj)}]
(ˆi+ˆj+ˆk)−3(2ˆi−3ˆj)
=−7ˆi+8ˆj−ˆk
→a×(→b×→c)∣∣→a×(→b×→c)∣∣=−7ˆi+8ˆj−ˆk√114
Required vector = 3→a×(→b×→c)∣∣→a×(→b×→c)∣∣=3−7ˆi+8ˆj−ˆk√114
Related Playlists
- BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise337videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGECHAPTER - DETERMINANTSEXERCISE - Question Bank23videos
DETERMINANTS
- BOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Question Bank25videos
DIFFERENTIAL EQUATIONS
Similar Questions
Find a vector which is perpendicular to each of the vectors in the following: ˆi−ˆj+ˆkand2ˆi+3ˆj−ˆk
View SolutionFind a vector which is perpendicular to each of the vectors in the following: ˆi+ˆj−2ˆkand2ˆi−2ˆj+ˆk
View SolutionFind a vector of magnitude 6 which is perpendicular to both the vectors 2ˆi−ˆj+2ˆkand4ˆi−ˆj+3ˆk.
View SolutionA unit vector perpendicular to both ˆi+ˆj+ˆk and 2ˆi+ˆj+3ˆk is
View SolutionFind a vector of magnitude 18 which is perpendicular to both the vectors 4ˆi−ˆj+3ˆk and −2ˆi+ˆj−2ˆk.
View SolutionThe unit vectors perpendicular to →A=2ˆi+3ˆj+ˆk and →B=ˆi−ˆj+ˆk is
View SolutionA vector of magnitude 12 units perpendicular to the plane containing the vector
4ˆi+6ˆj−ˆk and 3ˆi+8ˆj+ˆk isView SolutionFind the scalar components of a unit vector which is perpendicular to each of the vectors ˆi+2ˆj−ˆkand3ˆi−ˆj+2ˆk.
View SolutionFind unit vectors perpendicular to each of the vector in the following: 2ˆi−ˆj−ˆk,2ˆi−ˆj+3ˆk
View SolutionThe unit vector which is orthogonal to the vector 5ˆi+2ˆj+6ˆk and is coplanar with vectors 2ˆi+ˆj+ˆkandˆi−ˆj+ˆkis
View Solution