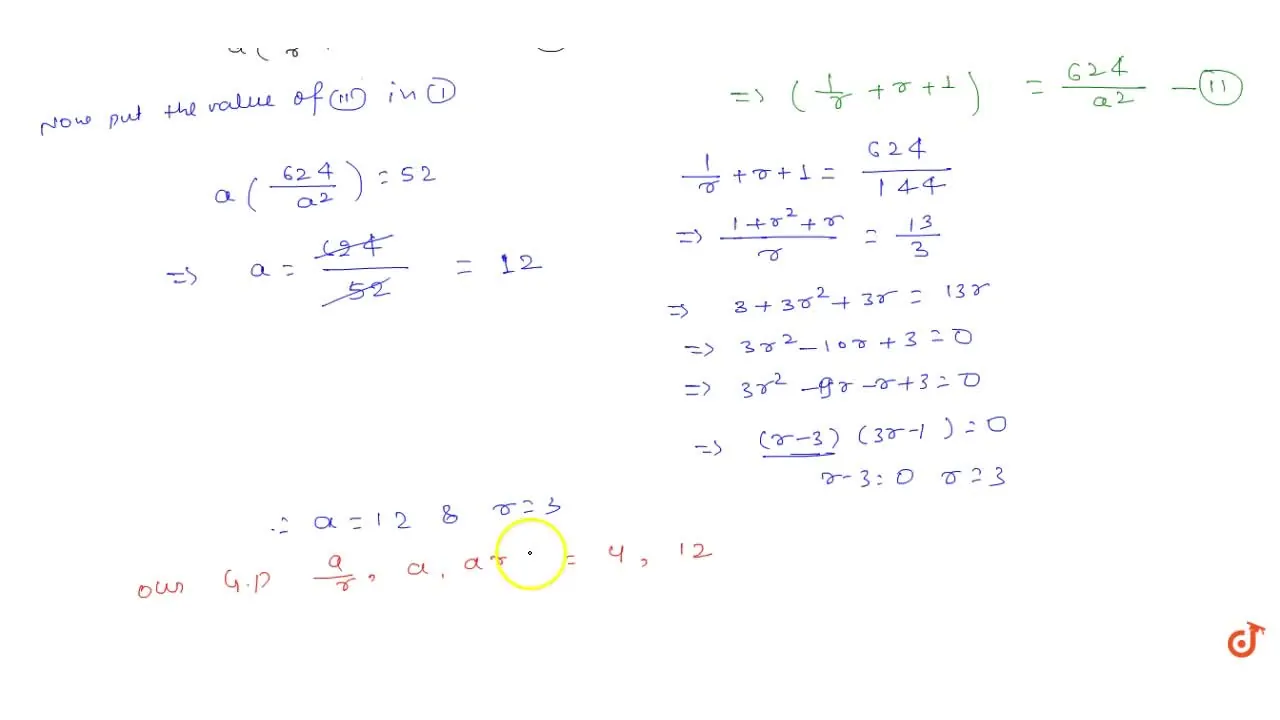Find three numbers in G.P. whose sum is 52 and the sum of whose products pairs is 624.
2, 12, 32
2,12, 72
4, 12, 36
None of these
The correct Answer is:C
Let the numbers are ar,aandar.
Then, ar+a+ar=52
⇒a(1r+1+r)=52→(1)
Also,
ar(a)+a(ar)+ar(ar)=624
⇒a2(1r+r+1)=624→(2)
⇒a(a(1r+r+1))=624
Using (1),
⇒52a=624
⇒a=12
Now, from (2),
⇒1+r+r2r=624a2
⇒1+r+r2r=624144
⇒1+r+r2r=133
⇒3+3r+3r2−13r=0
⇒3r2−10r+3=0
⇒3r2−9r−r+3=0
⇒(3r−1)(r−3)=0
⇒r=13orr=3
So, the three numbers are , 4,12and36.
Related Playlists
Similar Questions
Find three number in G.P. whose sum is 52 and the sum of whose products in pairs is 624
View SolutionFind three numbers in G.P. whose product is 729 and the sum of their products in pairs is 819.
View SolutionFind three numbers in G.P. whose sum is 13 and the sum of whose squares is 91.
View SolutionFind three numbers in A.P. whose sum is 9 and sum of whose cubes is 99.
View SolutionFind three numbers in A.P. whose sum is 9 and the sum of their squares is 35.
View SolutionFind three numbers in A.P. whose sum is 12 and product is 60.
View SolutionFind three numbers in A.P. whose sum is 12 and product is 48.
View SolutionFind three numbers in G.P. whose sum is 19 and product is 216.
View SolutionFind three numbers in A.P., whose sum is 15 and product is 80.
View SolutionFind four numbers in A.P. whose sum is 28 and the sum of whose squares is 216.
View Solution