For a set of five true or false questions, no student hs written the all correct answer and no two students have given the same sequence of answers. What is the maximum number of students in the class for this to be possible?
The correct Answer is:31
Clearly there are 2 ways of answering each of the 5 questions, i.e., true of false.
So, the total number of different sequences of answers =(2×2×2×2×2)=32.
There is only one all correct answer.
Maximum number of sequences of answers leaving aside the all correct answer =(32−1)=31.
Hence, the maximum possible number of students = 31.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - PERMUTATIONSEXERCISE - EXERCISE 8C10videos
PERMUTATIONS
- BOOK - RS AGGARWALCHAPTER - PERMUTATIONSEXERCISE - EXERCISE 8D28videos
PERMUTATIONS
- BOOK - RS AGGARWALCHAPTER - PERMUTATIONSEXERCISE - EXERCISE 8A14videos
PERMUTATIONS
- BOOK - RS AGGARWALCHAPTER - PARABOLAEXERCISE - EXERCISE-2210videos
PARABOLA
- BOOK - RS AGGARWALCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - EXERCISE 423videos
PRINCIPLE OF MATHEMATICAL INDUCTION
Similar Questions
For a set of five true/false questions, no student has written all correct answers, and no two students have given the same sequence of answers. What is the maximum number of students in the classes, for this to be possible?
View SolutionFollowing histogram depicts the range of heights of students in a class of 60 students. Study the same and answer the questions.
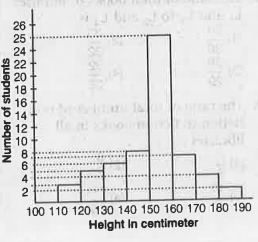
Which group contains maximum number of students ?View Solution
Knowledge Check
- Question 1 - Select One
For a set of four multiple choice questions with three options (multiple correct possible), no two students have given the same sequence of answers. What is the maximum number of students that sat for the test, for this to be possible, given that each student attempts all the questions. No student gives all the correct answers?
A4095B2400C1295D2500 - Question 2 - Select One
Following histogram depicts the range of heights of students in a class of 60 students. Study the same and answer the questions.

Group which contains maximum number of students isA130 - 140B150 - 160C140 - 150D160 - 170 - Question 3 - Select One
There are 60 questions in a question paper. If no two students solve the same combination of questions but solve equal number of questions, then the maximum number of student who appeared in the examination, is
A60C29B60C30C60C50Dnone of these
In a test, 6 questions are of the form ‘state, true or false’. No student has got all answers correct. Also, the answer of every student is different. Then the number of students appeared for the test
View SolutionThe following bar graph shows the number of students in a particular class of school. Then, answer the following questions.
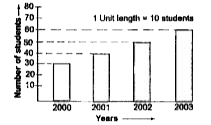
What is the number of students in the year 2003?View SolutionRead the following information carefully and answer the questions given below-
1000 students appeared in an examination Out of which 275 students passed in physics, 320 students passed in chemistry and 350 students passed in mathematics. 84 students passed in both chemistry and mathematics 60 students passed in both physics and mathematics, 50 students passed in both physics and chemistry and 34 students passed in all the three subjects.
What is the number of students who passed in at least two subjects ?View SolutionStudy the following histogram of marks in mathematics (out of 50) of students in a class and answer the following questions.
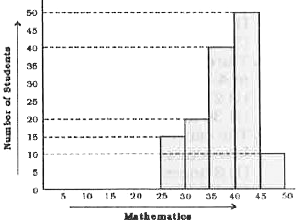
The total number of students in the class is :View SolutionThe following bar graph shows the number of students in a particular class of school. Then, answer the following questions.

What is the number of students in the year 2003?View Solution

