For any 3 sets A, B and C, prove that :
(i) A−(B∪C)=(A−B)∩(A−C)
(ii) A−(B∩C)=(A−B)∪(A−C)
(iii) A∩(B−C)=(A∩B)−(A∩C)
(iv) (A∪B)−C=(A−C)∪(B−C)
(v) A∩(BΔC)=(A∩B)Δ(A∩C).
(i) A−(B∪C)
=A∩(B∪C)' (∵X−Y=X∩Y')
=A∩(B'∩C')=(A∩B')∩(A∩C)
=(A−B)∩(A−C).
(ii) A−(B∩C)
=A∩(B∩C)'
=A∩(B'∪C')
=(A∩B')∪(A∩C') (From distributive law)
=(A−B)∪(A−C).
(iii) A∩(B−C)
=A∩(B∩C') (∵X−Y=X∩Y')
=(A∩B)∩C'(From associative law)
=ϕ∪[(A∩B)∩C']
=[(A∩B)∩A']∪[(A∩B)∩C']
=(A∩B)∩(A'∪C') (From distributive law)
=(A∩B)∩(A∩C)'
=(A∩B)−(A∩C) (∵X∩Y'=X−Y)
(iv) (A∪B)−C
=(A∪B)∩C' (X−Y=X∩Y')
=(A∩C')∪(B∩C') (From distributive law)
=(A−C)∪(B−C) (∵X∩Y'=X−Y)
(v) A∩(BΔC)
=A∩[(B−C)∪(C−B)]
[A∩(B−C)]∪[A∩(C−B)] (From distributive law)
=[(A∩B)−(A∩C)]∪[(A∩C)−(A∩B)]
=(A∩B)Δ(A∩C).
Topper's Solved these Questions
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1A
7 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1B
10 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise
32 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE
7 Videos
Similar Questions
For any two sets A and B, prove that :
(i) (A∩B)∪(A−B)=A
(ii) A∪(B−A)=A∪B.
View SolutionFor any two sets A and B, prove that :
(i) A−(A−B)=A∩B
(ii) A∩(A'∪B)=A∩B.
View SolutionProve A∪(B∩C)=(A∪B)∩(A∪C)
View SolutionFor sets A, B,C , show that (A−B)∪(A−C)=A−(B∪C)
View SolutionProve (A∩B)'=(A'∪B')
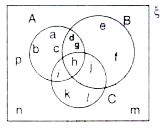
View SolutionUse the given diagram to find:
(i) A∪(B∩C)
(ii) B−(A−C)
(iii) A-B
(iv) A∩B'
is A∩B'=A−B?
View SolutionIf A = {1, 2, 3, 4, 5}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}, verify:
(i) A−(B∪C)=(A−B)∩(A−C)
(ii) A−(B∩C)=(A−B)∪(A−C)
View SolutionIf A = {5, 6, 7, 8, 9}, B={x:3<x<8 and x∈W} and C={x:x≤5 and x∈N}. Find :
(i) A∪B and (A∪B)∪C
(ii) B∪C and A∪(B∪C)
(iii) A∩B and (A∩B)∩C
(iv) B∩C and A∩(B∩C)
Is (A∪B)∪C=A∪(B∪C)?
Is (A∩B)∩C)=A∩(B∩C)?
View SolutionIf A{1,2,3},B={3,4}andC={4,5,6}, then find the each of the following :
(i) A∩(B∪C)
(ii) (A−B)∪C
(iii) (A∪B)−C
(iv) (A∩B)∪C.
View SolutionIf A and B are stes, then A∩(A∪B)=
View Solution
