For any scalar prove that .
Video Solution
Text Solution
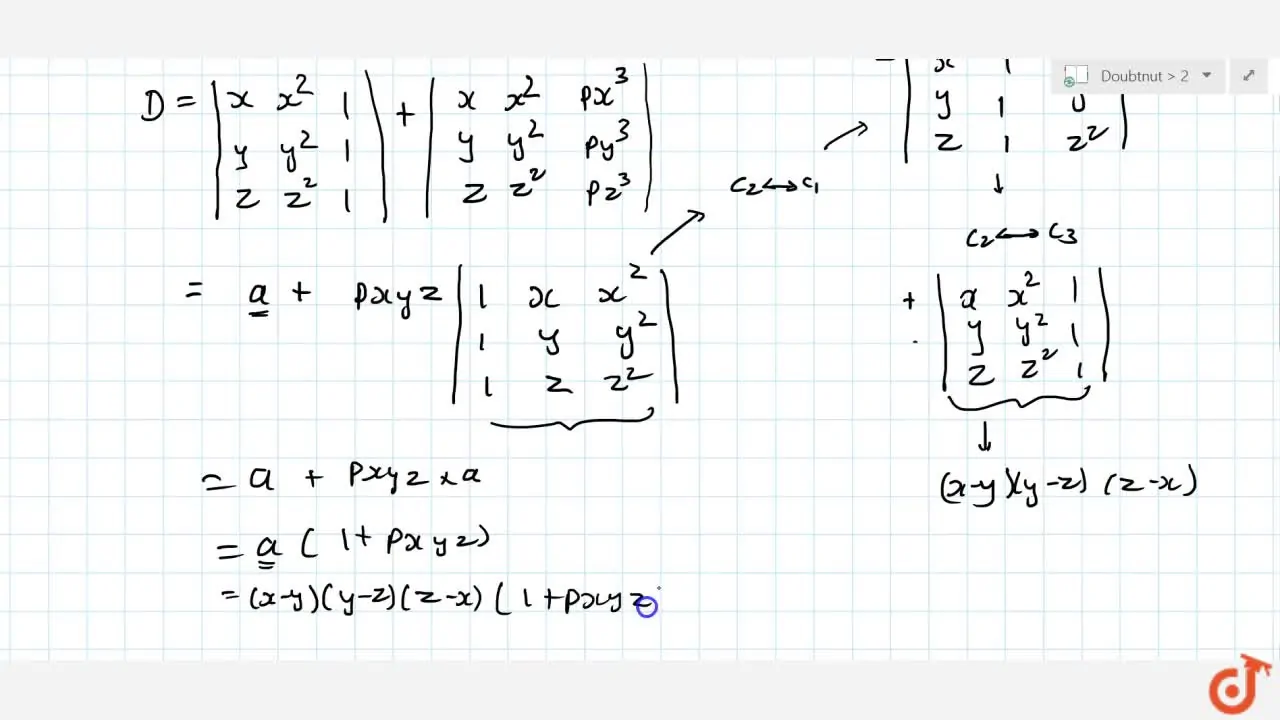
LHS $$=\left|\begin{array}{lll}x & x^{2} & 1+p x^{3} \\ y & y^{2} & 1+p y^{3} \\ z & 2^{2} & 1+p z^{3}\end{array}\right|$$
By splitting into two parts, we get
$$=\left|\begin{array}{llllll}x & x^{2} & 1 & x & x^{2} & p x^{3} \\ y & y^{2} & 1+y & y^{2} & p y^{3} \\ z & z^{2} & 1 & z & z^{2} & p z^{3}\end{array}\right|$$
In second determinant, replacing and and then with ]
$$
=(1+\operatorname{pxy} y)\left|\begin{array}{lll}
x & x^{2} & 1 \\
y & y^{2} & 1 \\
z & z^{2} & 1
\end{array}\right|
$$
By applying , we get
$$
\begin{aligned}
&=(1+ pxyz)\left|\begin{array}{ccc}
x-y & (x-y)(x+y) & 0 \\
y-z & (y-2)(y+z) & 0 \\
2 & 2^{2} & 1
\end{array}\right| \\
&=(1+ pxyz)(x-y)(y-2)\left|\begin{array}{ccc}
1 & x+y & 0 \\
1 & y+z & 0 \\
z & z^{2} & 1
\end{array}\right|
\end{aligned}
$$
By expanding the determinant, we get
$$
\begin{array}{ll}
\Rightarrow & (1+p x y z)(x-y)(y-z)[y+z-x-y] \\
\Rightarrow \quad & (1+p x y z)(x-y)(y-z)(z-x)
\end{array}
$$
Hence Proved
|
Updated on:21/07/2023
Related Playlists
Similar Questions
For any scalar p prove that =∣∣×21+px3yy21+py3zz21+pz3∣∣=(1+pxyz)(x−y)(y−z)(z−x) .
View SolutionProve that ⎡⎢⎣xx21+px3yy21+py3zz21+pz3⎤⎥⎦=(1+pxyz)(x−y)(y−z)(z−x)
View SolutionShow that : ∣∣xyzx2y2z2x3y3z3∣∣=xyz(x−y)(y−z)(z−x).
View SolutionProve that x3+y3+z3−3xyz=12(x+y+z)[(x−y)2+(y−z)2+(z−x)2]
View SolutionWithout expanding as far as possible, prove that ∣∣ ∣ ∣∣111xyzx3y3z3∣∣ ∣ ∣∣=(x−y)(y−z)(z−x)(x+y+z).
View SolutionProve that ∣∣ ∣ ∣∣xyzx2y2z2yzzxxy∣∣ ∣ ∣∣=∣∣ ∣ ∣∣111x2y2z2x3y3z3∣∣ ∣ ∣∣
View Solutionx+y-z=1
3x+y-2z=3
x-y-z=-1View SolutionIf x+y+z=xyz, prove that 3x−x31−3x2+3y−y31−3y2+3z−z31−3z2=3x−x3(1−3x)2⋅3y−y3(1−3x)2⋅3z−z3(1−3z)2.
View SolutionIf ∣∣ ∣ ∣∣xx21+x3yy21+y3zz21+z3∣∣ ∣ ∣∣=0 then relation of x,y and z is
View SolutionProve that :
=2∣∣ ∣ ∣∣111xyrzx2y2z2∣∣ ∣ ∣∣=(x−y)(y−z)(z−x)View Solution