For y2=4x, pormals at P, Q, Rare concurrent at a point (3,0), then for ΔPQR
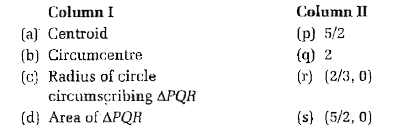
The correct Answer is:(a)→(r),(b)→(s),(c)→(p),(d)→(q)
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - THE PARABOLA EXERCISE - Problem Set (3) (TRUE AND FALSE)4videos
THE PARABOLA
- BOOK - ML KHANNACHAPTER - THE PARABOLA EXERCISE - Problem Set (3) (FILL IN THE BLANKS)5videos
THE PARABOLA
- BOOK - ML KHANNACHAPTER - THE PARABOLA EXERCISE - Problem Set (2) (FILL IN THE BLANKS)5videos
THE PARABOLA
- BOOK - ML KHANNACHAPTER - THE HYPERBOLA EXERCISE - SELF ASSESSMENT TEST4videos
THE HYPERBOLA
- BOOK - ML KHANNACHAPTER - THEORY OF QUADRATIC EQUATIONS EXERCISE - Self Assessment Test27videos
THEORY OF QUADRATIC EQUATIONS
Similar Questions
Let P,Q,R be three points on a parabola, normals at which are concurrent, the centroid of ΔPQR must lie on
View SolutionNormal at a point P(a,-2a) intersects the parabola y2=4ax at point Q.If the tangents at P and Q meet at point R,if the area of triangle PQR is 4a2(1+m2)3mλ.Then find λ
View Solution
Knowledge Check
- Question 1 - Select One
Consider the parabola y2=4x, let P and Q be two points (4,−4) and (9,6) on the parabola. Let R be a moving point on the arc of the parabola whose x-coordinate is between P and Q. If the maximum area of triangle PQR is K, then (4K)1/3 is equal to
A1B2C5D7
Match the conditions/expression in Column I With statement in Column II. Normals at P,Q,R are drawn to y2=4x which intersect at (3,0). Then,
column Icolumn IIA.Area ofΔPQRp.2B.Radius of circumcircle ofΔPQRq.52C.Centroid ofΔPQRr.(52,0)D.Circumcentre ofΔPQRs.(23,0)View SolutionIn a △PQR mark
the points X, Y, Z in the interior of △ PQRView SolutionThe normals at P, Q, R on the parabola y2=4ax meet in a point on the line y=c. Prove that the sides of the triangle PQR touch the parabola x2=2cy.
View SolutionTangents are drawn to the hyperbola 4x2−y2=36 at the points P and Q. If these tangents intersect at the point T(0,3) and the area (in sq units) of ΔTPQ is a√5 then a=
View SolutionIf the normals to the curve y=x2 at the points P,QandR pas thrugh the points (0,32), then find circle circumsecribing the triangle PQR.
View SolutionFrom the point (3 0) 3- normals are drawn to the parabola y2=4x. Feet of these normal are P ,Q ,R then area of triangle PQR is
View SolutionFrom a variable point R on the line y = 2x + 3 tangents are drawn to the parabola y2=4ax touch it at P and Q point. Find the locus of the centroid of the triangle PQR.
View Solution

