From the given figure, answer the following questions
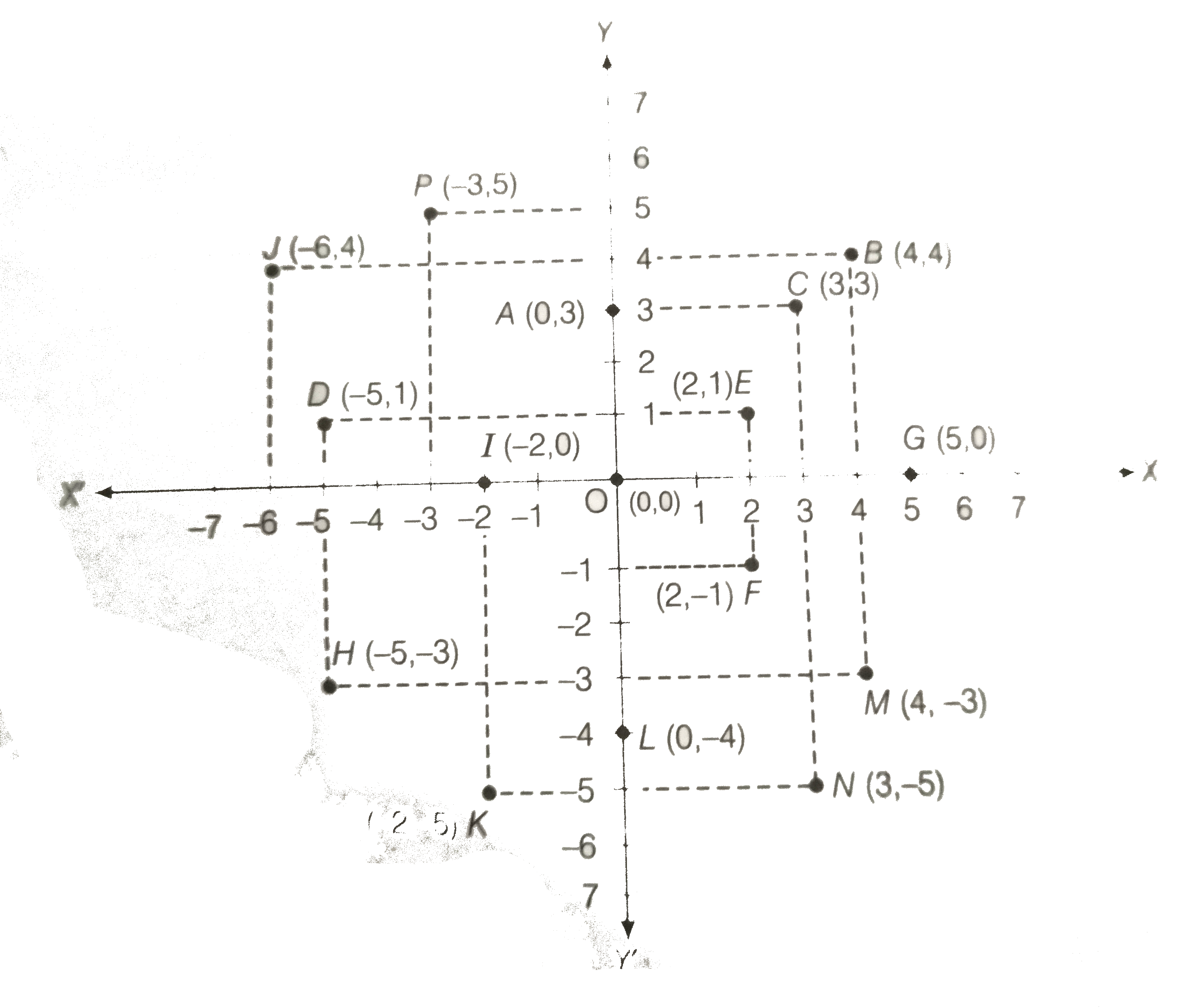
(i) Write the points whose abscissa is 0.
(ii) Write the points whose ordinate is 0.
(iii) Write the points whose abscissa is -5.
(i) We know that, the point whose abscissa is 0 will lie on Y-axis . So, the required points whose abscissa is 0 are A , L and O.
(iii) Here, abscissa '-5' is negative , which shows that point with abscissa -5 will lie in II and III quadrants. So, the required points whose abscissa is -5, are D and H.
Note We know that, origin O is the intersection point of both axes. So, we can consider it on X-axis as well as on Y-axis.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.3 Short Answer Type Questions12videos
COORDINATE GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Long Answer Type Questions8videos
HERON'S FORMULA
Similar Questions
A point whose abscissa is −3 and ordinate 2 lies in
View SolutionThe point whose ordinate is 4 and which lies on y-axis is
View SolutionThe points whose abscissa and ordinate have different signs will lie in
View SolutionEquation of normal to y2 = 4x at the point whose ordinate is 4 is
View SolutionUse the graph given along side, to find the co ordinates of the point (s) satisfying the given conditions:
(i) The abscissa is 2 (ii) The ordinate is 0 (iii) The ordinate is 3 (iv) The ordinate is 2 (v) The abscissa is 5 (vi) The abscissa is equal to the ordinate (vii) The ordinate is half of the abscissa
 View Solution
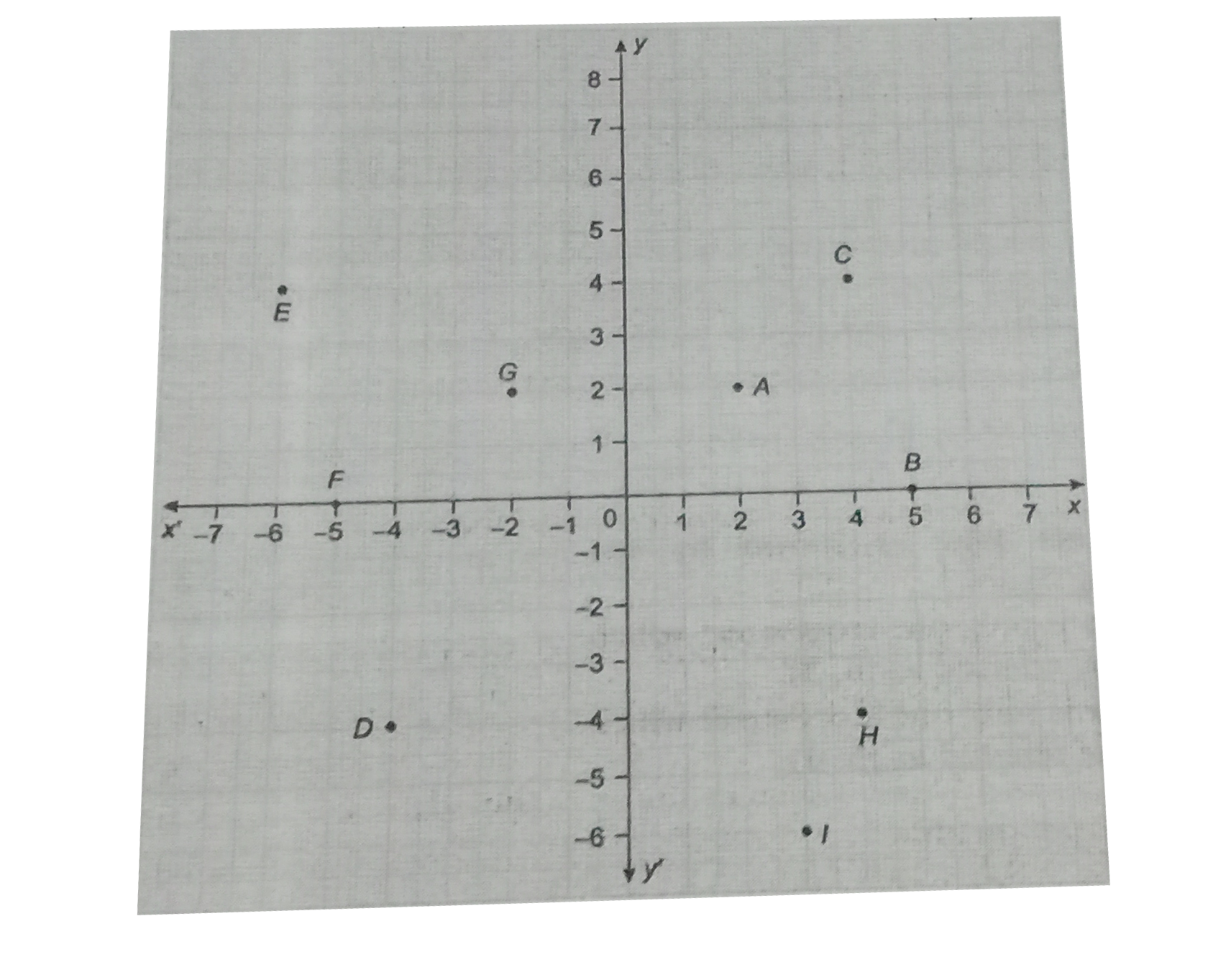
View SolutionUse the given graph to find the co-ordinates of the points, satisfying the given condition.
(i) Whose abscissa is 2
(ii) Whose ordinates is 4
(iii) Whose abscissa is 5
(iv) Whose ordinates is -6
(v) Whose abscissa is -4
(vi) Whose abscissa is 4
 View Solution
View SolutionThe length of the subtangent to the parabola y2=16x at the point whose abscissa is 4, is
View SolutionFind the co-ordinates of a point whose absicissa is 10 and its distance from the point (2, -3) is 10 units.
View SolutionWrite the slope of the line whose inclination is:
0∘View SolutionFind the equation of tangents of the circle
x2+y2−10=0 at the points whose
abscissae are 1.View Solution
