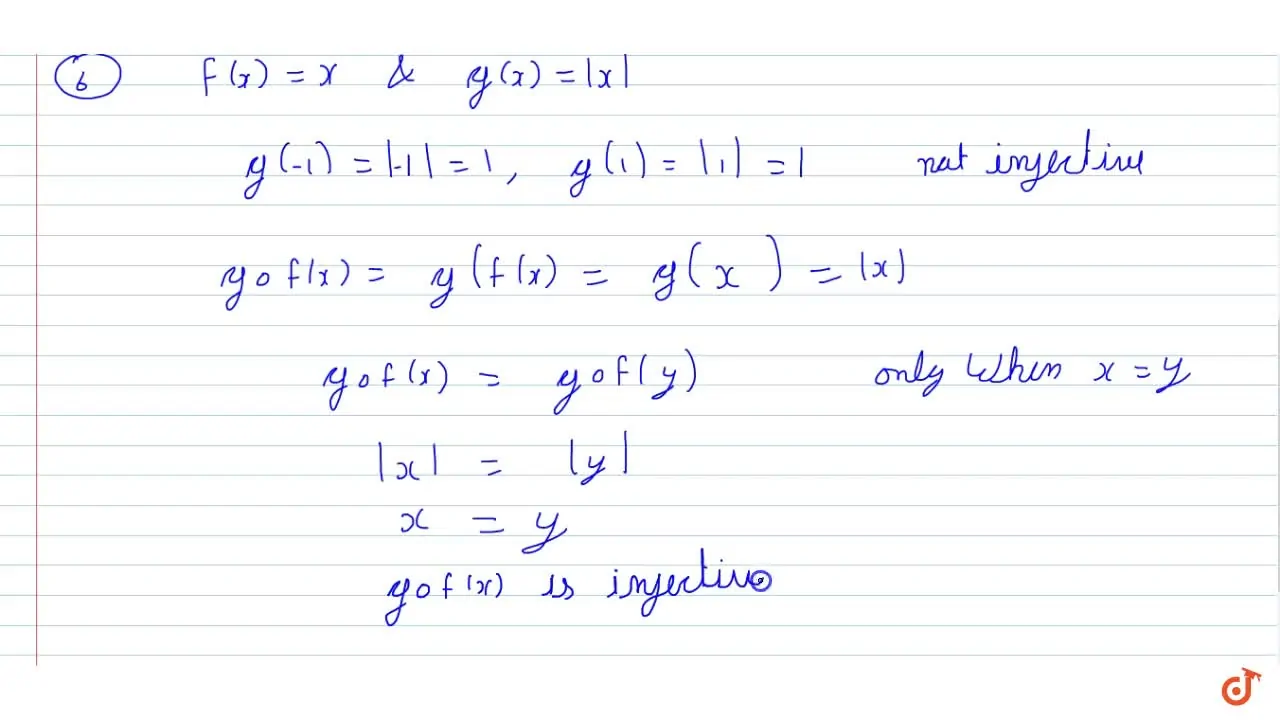Give examples of two functions f:N→Z and g:Z→Zsuch that gof is injective but g is not injective. (Hint: Consider f(x)=x and g(x)=|x|)
A function f(x) is injective when,
f(x1)=f(x2) only if x1=x2.
Let f(x)=xandg(x)=|x|.
Here, g(1)=g(−1)=1.
So, g(x) is not injective.
Now, gof=gof(x)=g(f(x))=g(x)=|x|
But, f:N→Z. It means x can not be negative, so,
gof(x1)=gof(x2) only when x1=x2.
∴gof is injective.
Similar Questions
Give examples of two functions f:N→Z and g:Z→Zsuch that gof is injective but g is not injective. (Hint: Consider f(x)=x and g(x)=|x|)
View SolutionGiven examples of two functions f:N→N and g:N→Nsuch that gof is onto but f is not onto. (Hint: Consider f(x)=x+1 and g(x)=|x|) .
View SolutionLet f:A→B;g:B→A be two functions such that gof=IA. Then; f is an injection and g is a surjection.
View SolutionLet f:A→B;g:B→A be two functions such that fog=IB. Then; f is a surjection and g is an injection.
View SolutionLet f:Z→Z be defined by f(x)=x+2. Find g:Z→Z such that gof=IZ .
View SolutionIf f(x)=cosx+sinx and g(x)=x2−1, then g(f(x)) is injective in the interval
View SolutionConsider the functions f:X→Yandg:Y→Z then which of the following is/are incorrect?
View SolutionIf two real functions f and g such that f(x)=x2 and g(x)=[x], then the value of f(−2)+g(−12) is
View SolutionClassify f:Z→Z , defined by f(x)=x−5 as injection, surjection or bijection.
View SolutionIf the function f(x)=3x+aandg(x)=4x+9 are such that (g∘g)(x)=(g∘f)(x), then: a=
View Solution