Question

Given $C_1<C_2<C_3<C_4<C_5$ and the function $y=f\left(x\right)$ is twice differentiable .
$f\text{'}\left(x\right)>0\text{for}x\in (C_2,C_4),f\text{'}\left(C_2\right)=f\text{'}\left(C_4\right)=0$ and $f\text{'}\left(x\right)<0$ for all the remaining values. Also $f\text{'}\text{'}\left(C_1\right)=f\text{'}\text{'}\left(C_3\right)=f\text{'}\text{'}\left(C_5\right)=0$ and $f\text{'}\text{'}\left(x\right)>0$ for $x\in (C_1,C_3)\cup (C_5,\infty )$ and $f\text{'}\text{'}\left(x\right)<0$ for remaining values. Answer the following:
(i) What is the minimum number of asymptotes parallel to the x-axis for $y=f\left(x\right)$?
(ii) What is the maximum number of asymptotes parallel to the x-axis of $y=f\left(x\right)$ ?
(iii) If the range of $y=f\left(x\right)$ is $[a,b],a,b\in R$, then what is the minimum number of asymptotes parallel to the x-axis of $y=f\left(x\right)$ ?
(iv) If the range of $y=f\left(x\right)$ is non-finite interval, then what is the maximum number of asymptotes parallel to the x-axis ?

Explanation

(i) If the graph of `y=f(x)` is as given in the figure, it will not have any asymptote.

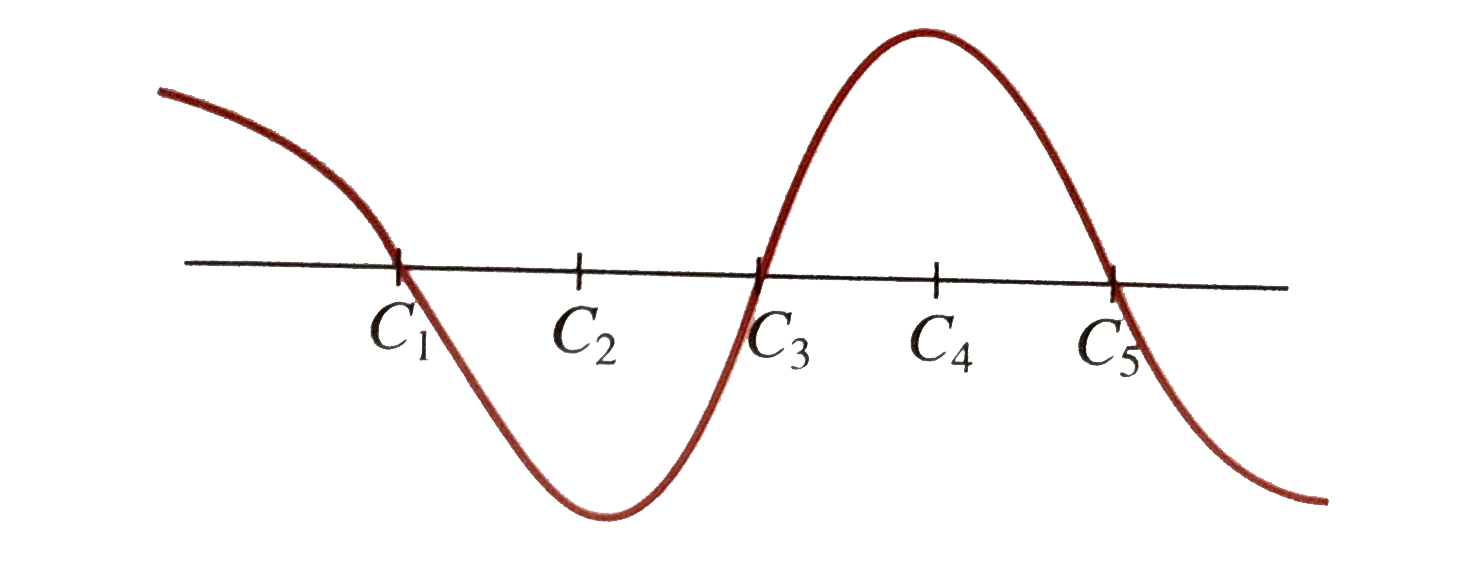
(ii) If the graph is as given in the figure, then it will have two asymptotes.

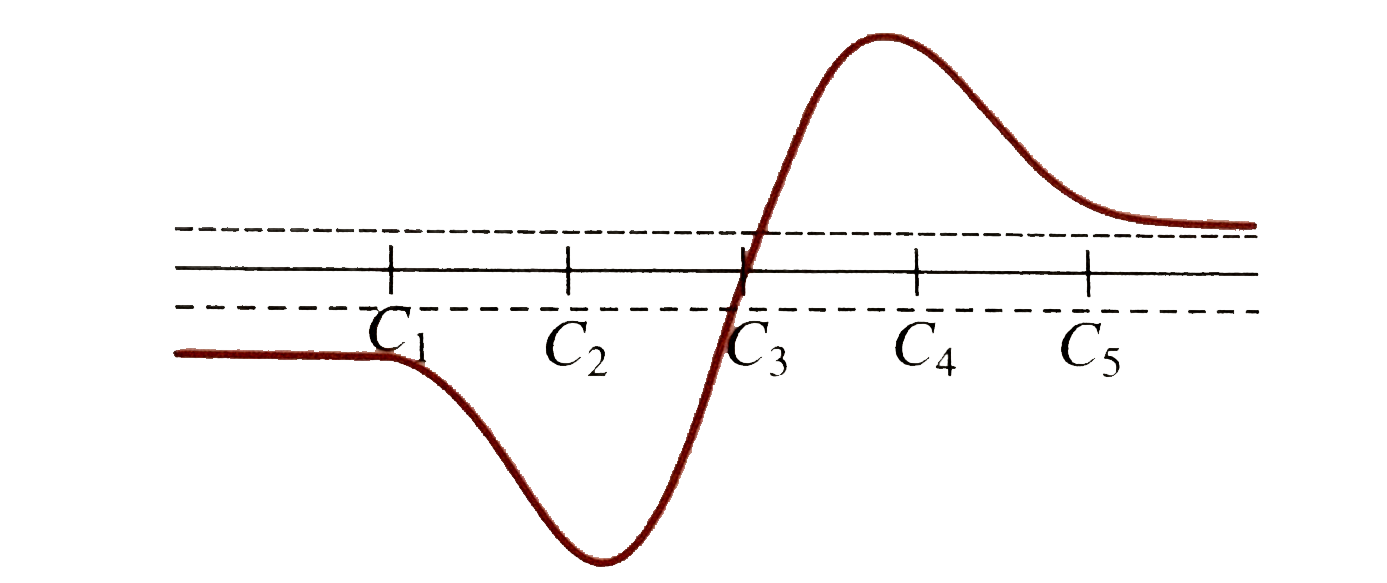
(iii) Since the range is a finite interval , the function must have at least one asymptote.

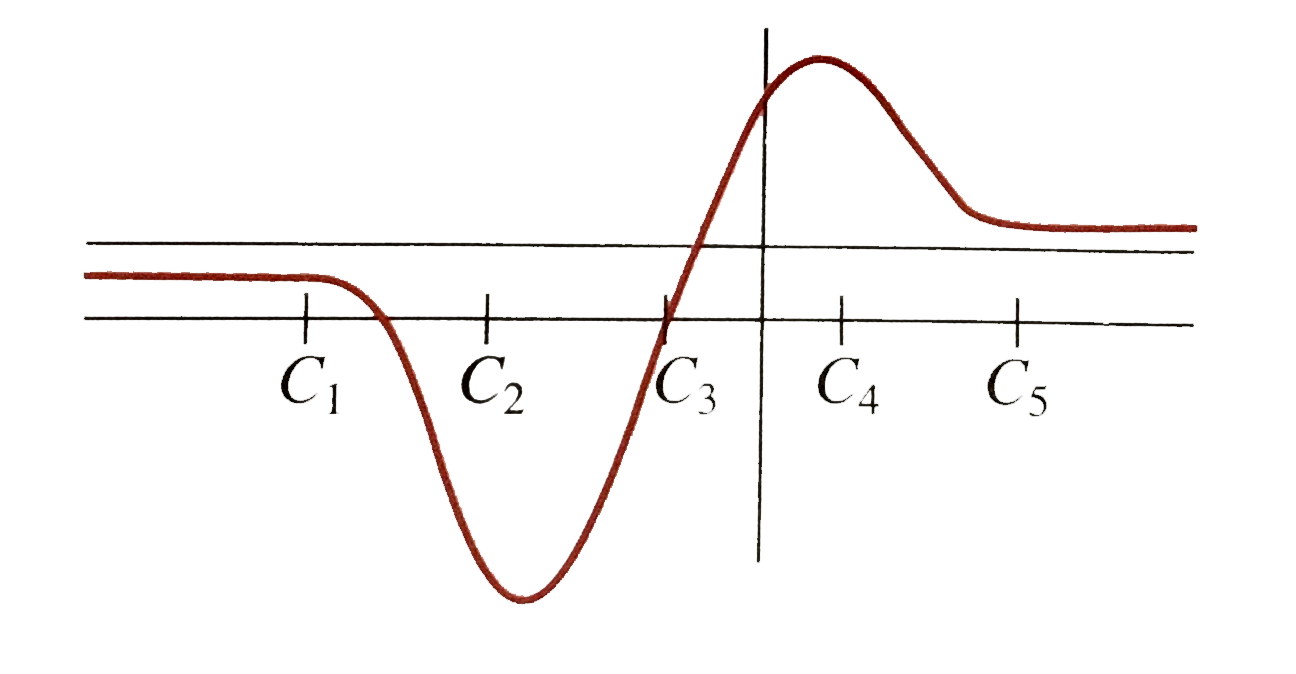
(iv) For the range to be an infinite interval, it should be non-bounded from at least one side.
So the maximum number of asymptotes is one.