Given f(x)=3x+2. Find f−1(x)
To find the inverse of the function f(x)=3x+2, we will follow a systematic approach. Here are the steps:
Step 1: Replace f(x) with y
We start by writing the function in terms of y:
y=3x+2
Step 2: Swap x and y
To find the inverse, we swap x and y:
x=3y+2
Step 3: Isolate y
Now, we need to isolate y in the equation x=3y+2.
1. Subtract 2 from both sides:
x−2=3y
2. Divide both sides by 3:
y=x−23
Step 4: Write the inverse function
Now that we have isolated y, we can express the inverse function:
f−1(x)=x−23
Thus, the inverse of the function f(x)=3x+2 is:
f−1(x)=x−23
---
We start by writing the function in terms of y:
y=3x+2
To find the inverse, we swap x and y:
x=3y+2
Now, we need to isolate y in the equation x=3y+2.
x−2=3y
y=x−23
Now that we have isolated y, we can express the inverse function:
f−1(x)=x−23
f−1(x)=x−23
Topper's Solved these Questions
Similar Questions
If {(3,2),(4,2),(3,1),(7,1),(2,3)} is to be a function, which one of the following must be removed from the set?
View SolutionIf xa⋅(xa+1)a⋅(xa)1−a=xk, then k=
View Solution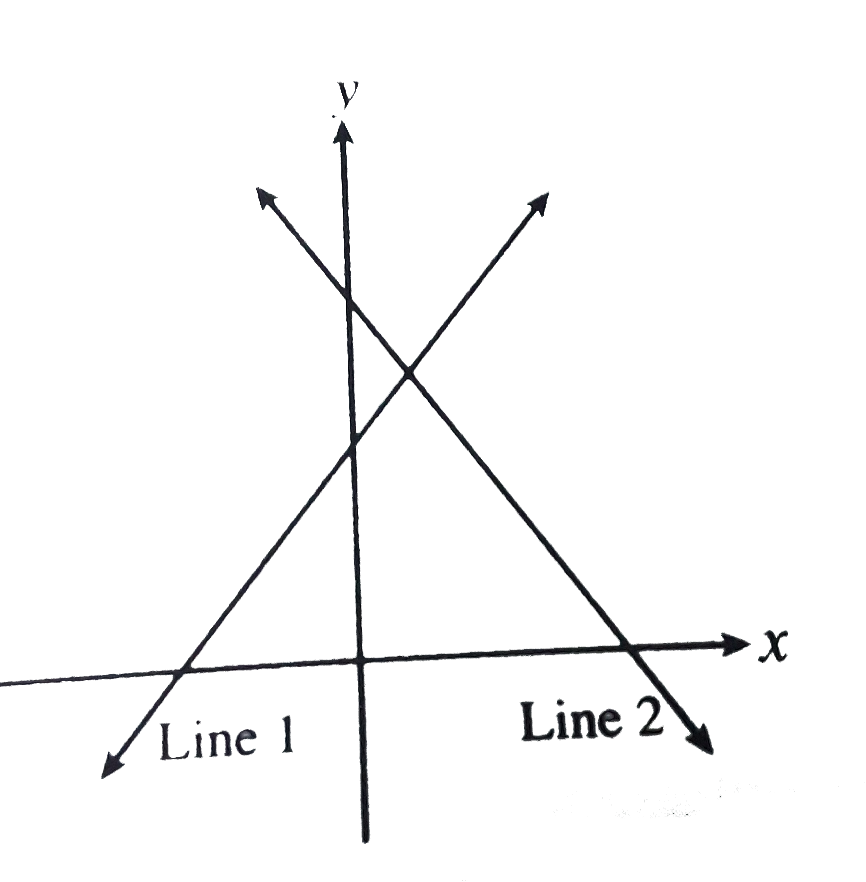
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?
View SolutionIf f(x)=x^(2)+3x-5, find f(0),f(1) and f((1)/(2))
View SolutionGiven f(x) = 3x - 9 , find f(-1), f(3), f(x+h) and f(x2−1).
View SolutionGiven that f'(x)=4x3−3x2+2x−1 find f(x) if f(0)=0.
View Solution(i) If f(x)=3x4−5x2+7, find f(x−1)
(ii) If f(x)=x2−3x+4, then find the values of x satisfying f(x)=f(2x+1)
View SolutionGiven f(x+1) = 3x +5 , evaluate f(-2) and f(x)
View SolutionGiven the function f(x)=5x2+12−x
Find f(3x),f(x3),3f(x),[f(x)]3.
View SolutionFind f(x) if f(x+1)=x2−3x+2
View SolutionIf f(x)=x2+3x+10, find f1(1).
View SolutionIf f(x)=3x2−x+1, then find f(−2).
View SolutionIf f(x)=3x2+2x+1, then find f(x−1)
View SolutionIf f(x)=3x2−x+1, then find f(−1)
View SolutionIf f(x)=x2−3x+1, then find f(12)
View Solution
