Given the graph of f(x), draw the graph each one of the following functions :
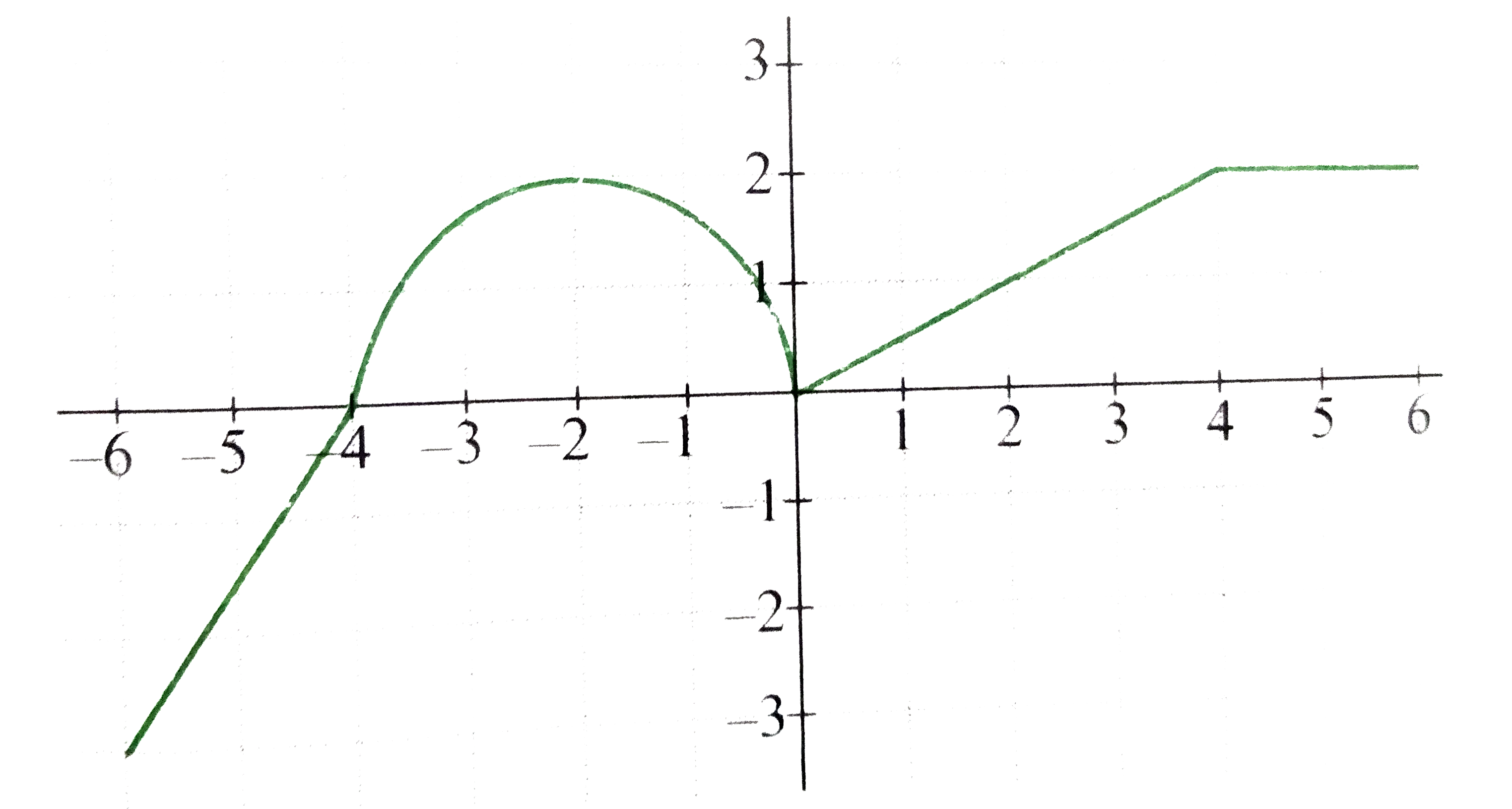
(a) y=f(x)+3 (b) y=−f(x)+2
(c ) y=f(x+1)−2 (d) y=−f(x−1)
(e ) y=f(−x) (f) y=f(|x|)
(g) y=f(1−x)
(a) For y=f(x)+3, shift the graph of y=f(x),3 units upward.
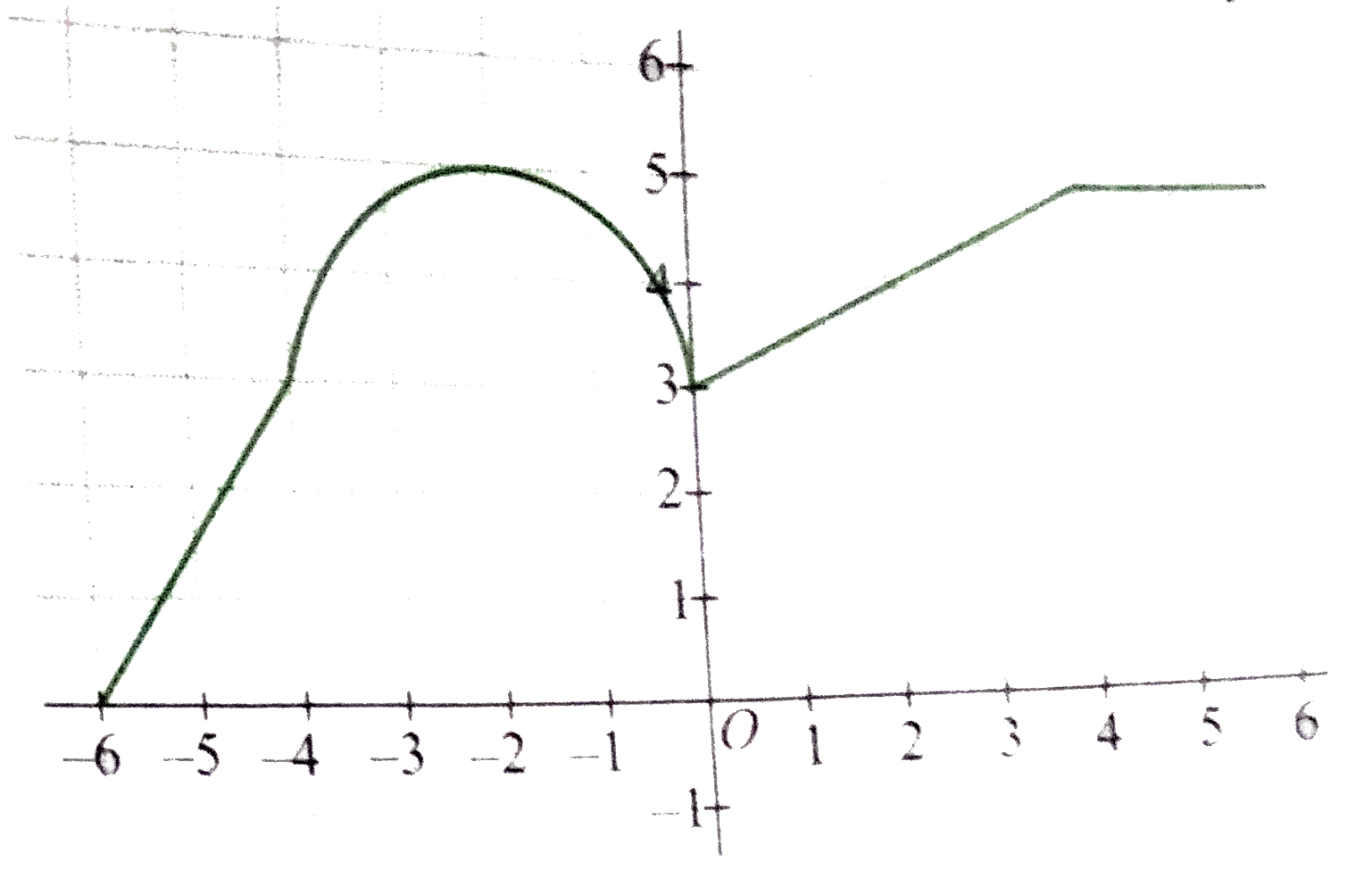
(b) y=−f(x)+2
First graph of y=f(x) about x-axis to get y=−f(x).
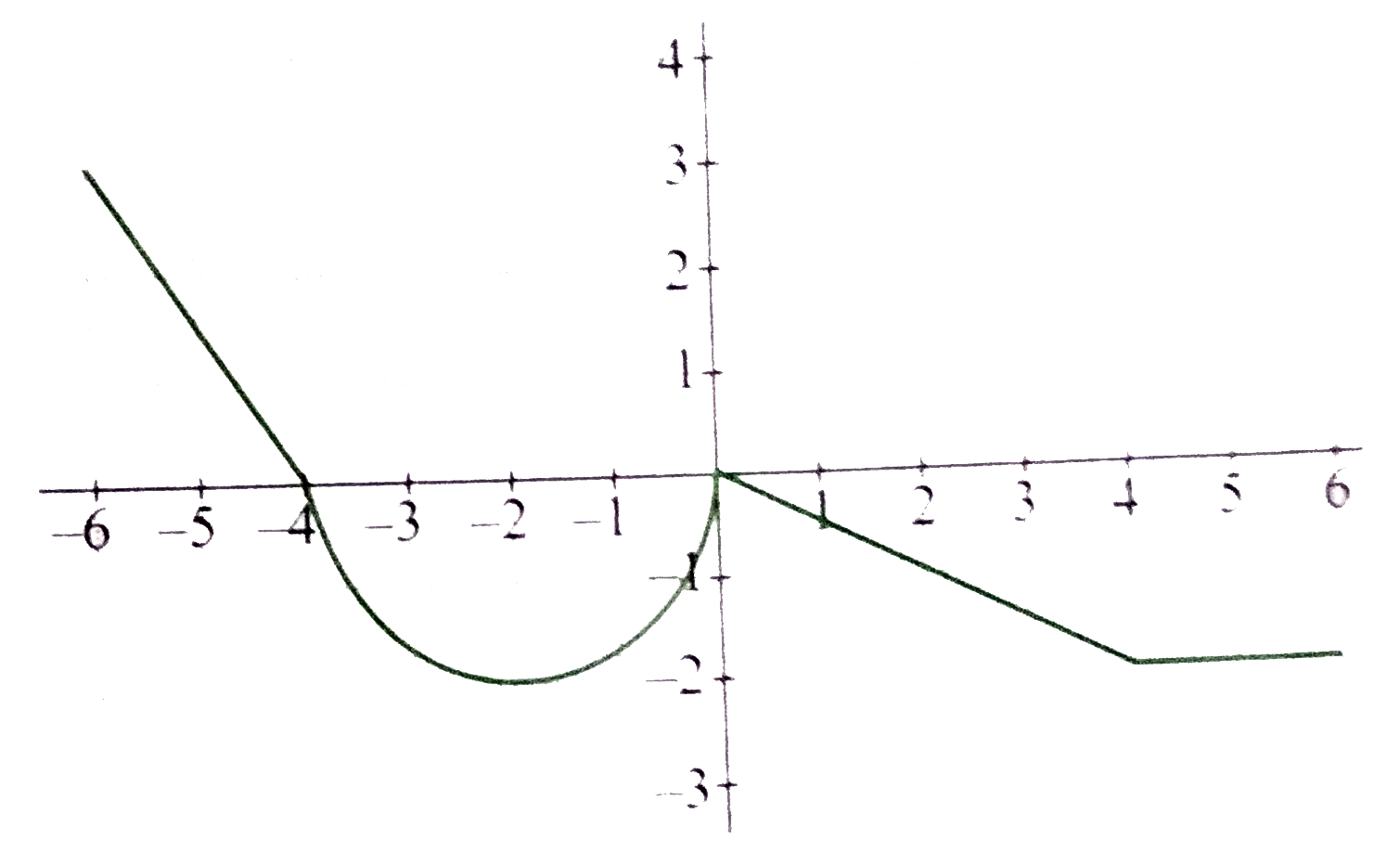
Now, shift the above graph 2 units upward to get y=2−f(x).
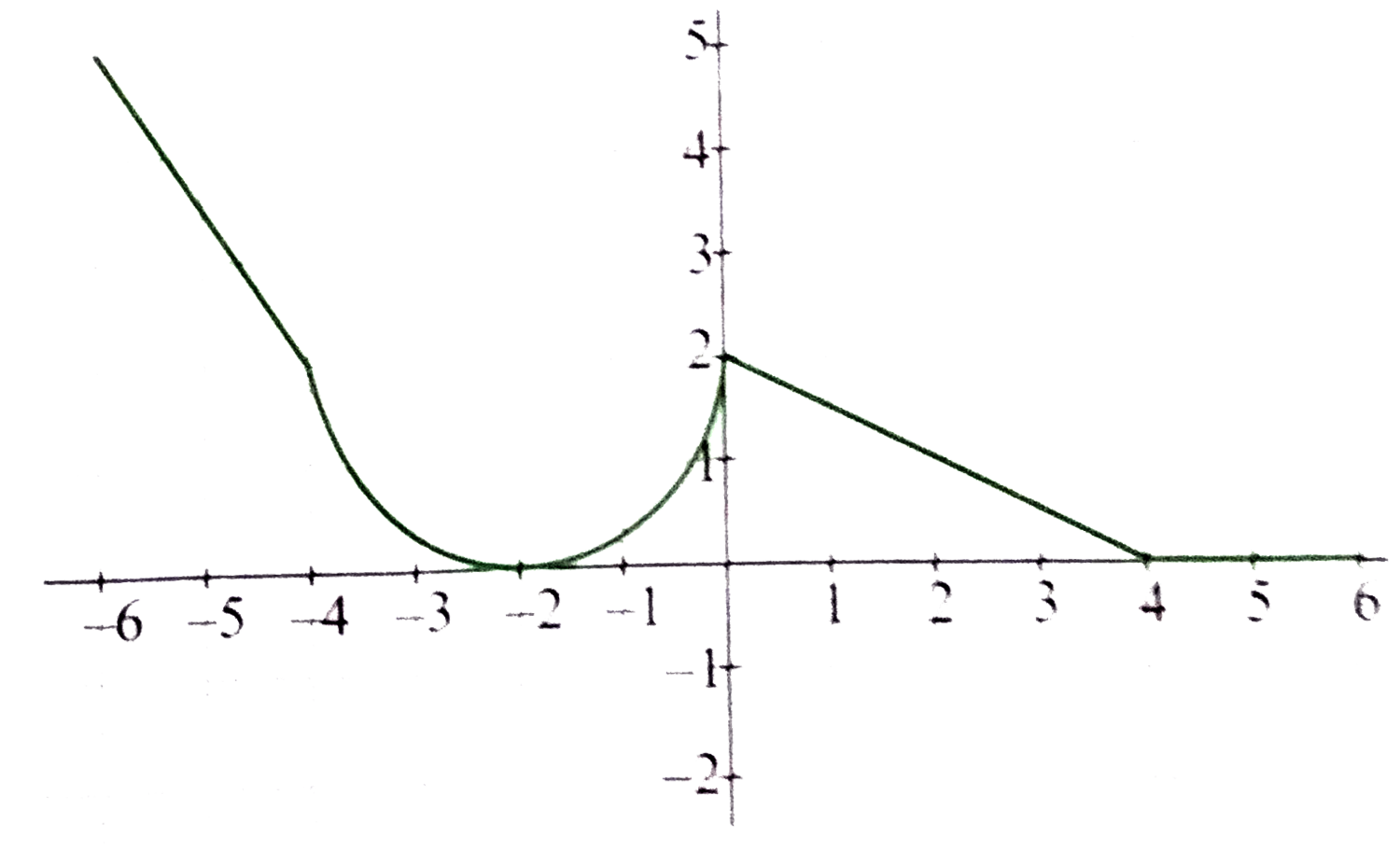
(c ) y=f(x+1)−2
First shift the graph of y=f(x), 1 units left to get y=f(x+1).
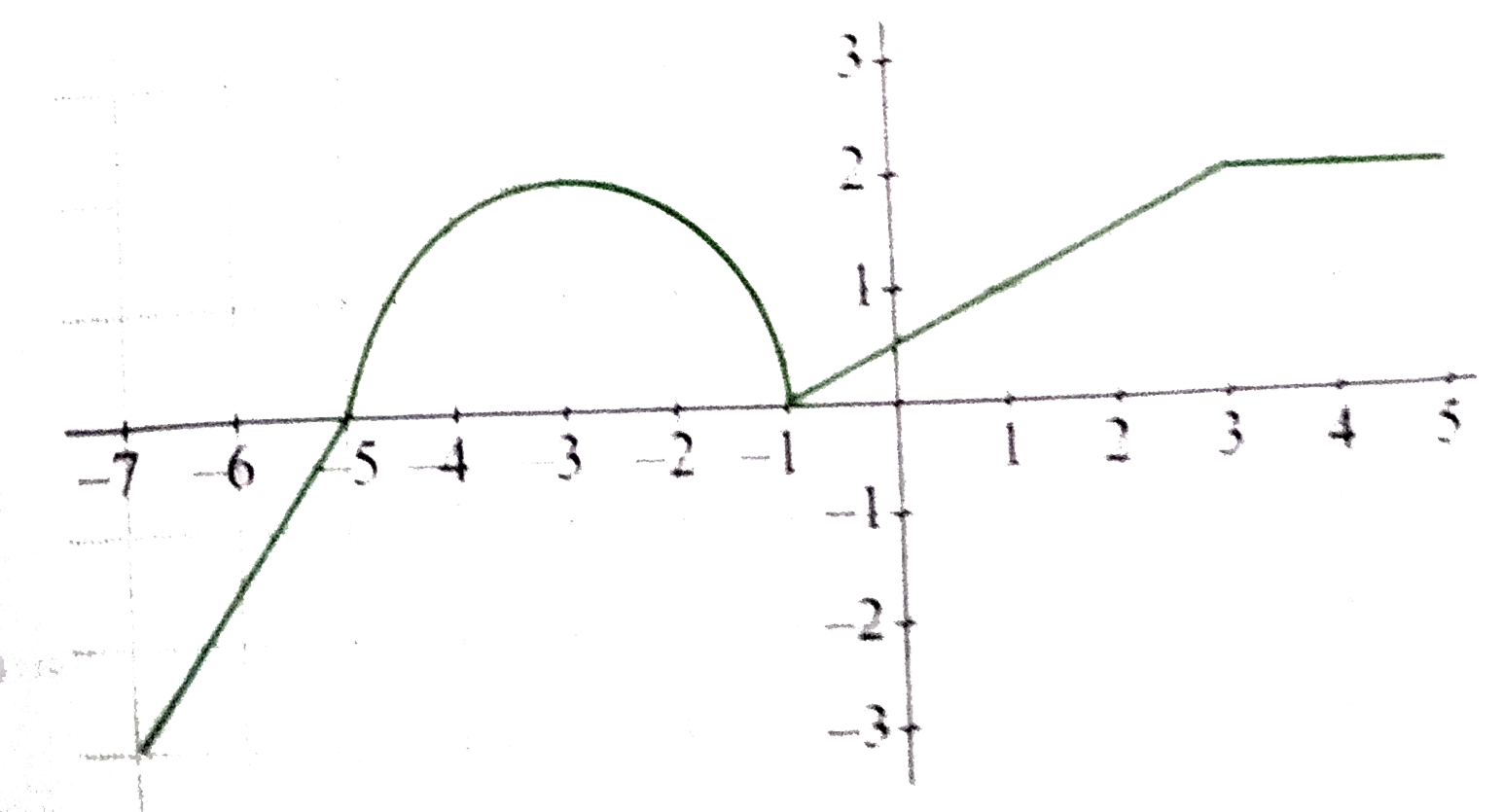
Now shift the above graph 2 units downward to get
y=f(x+1)−2.
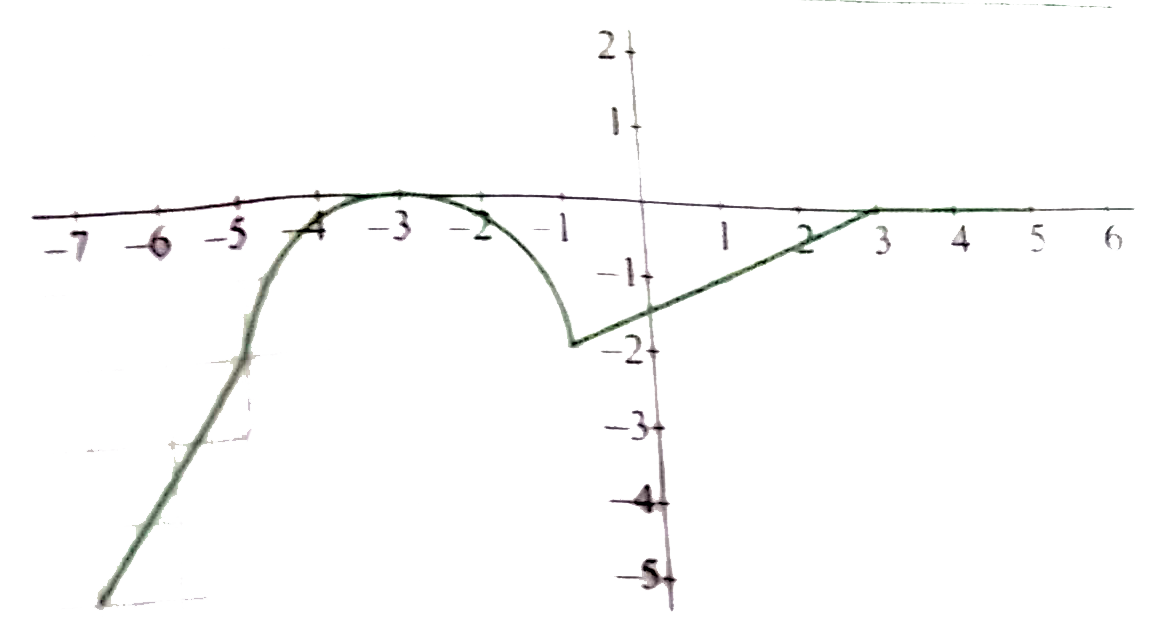
(d) y=−f(x−1)
First shift the graph of y=f(x), 1 unit right to get y=f(x−1).

Now, flip the above graph about x- axis to get y=−f(x−1).
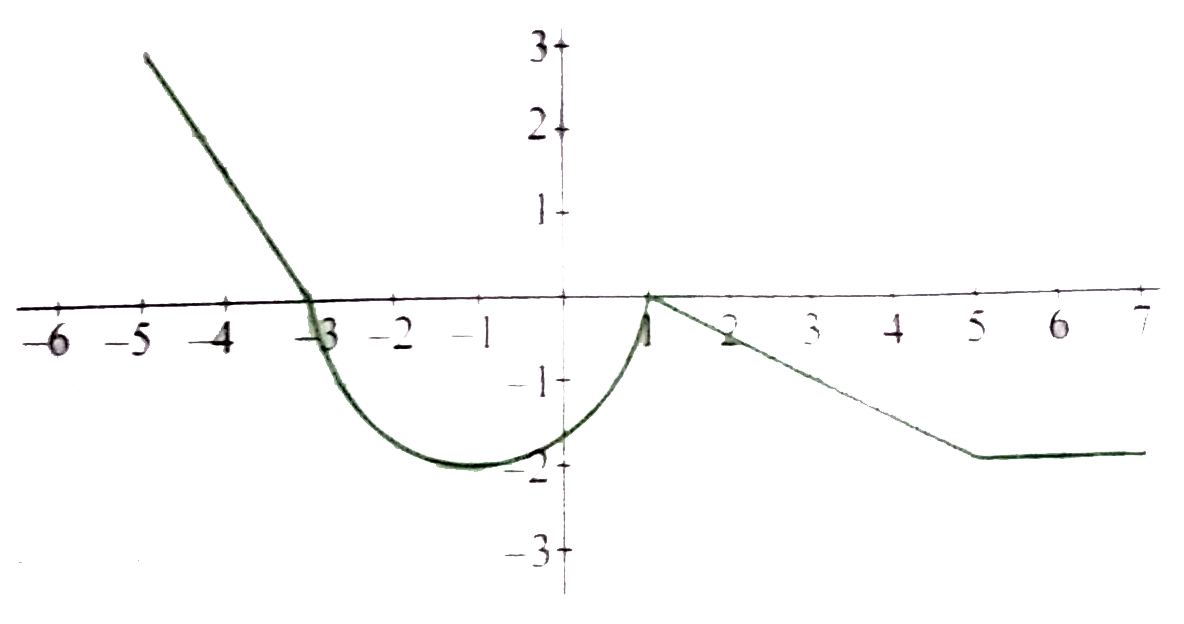
(e ) y=f(−x)
Flip the graph about y-axis to get y=f(−x).
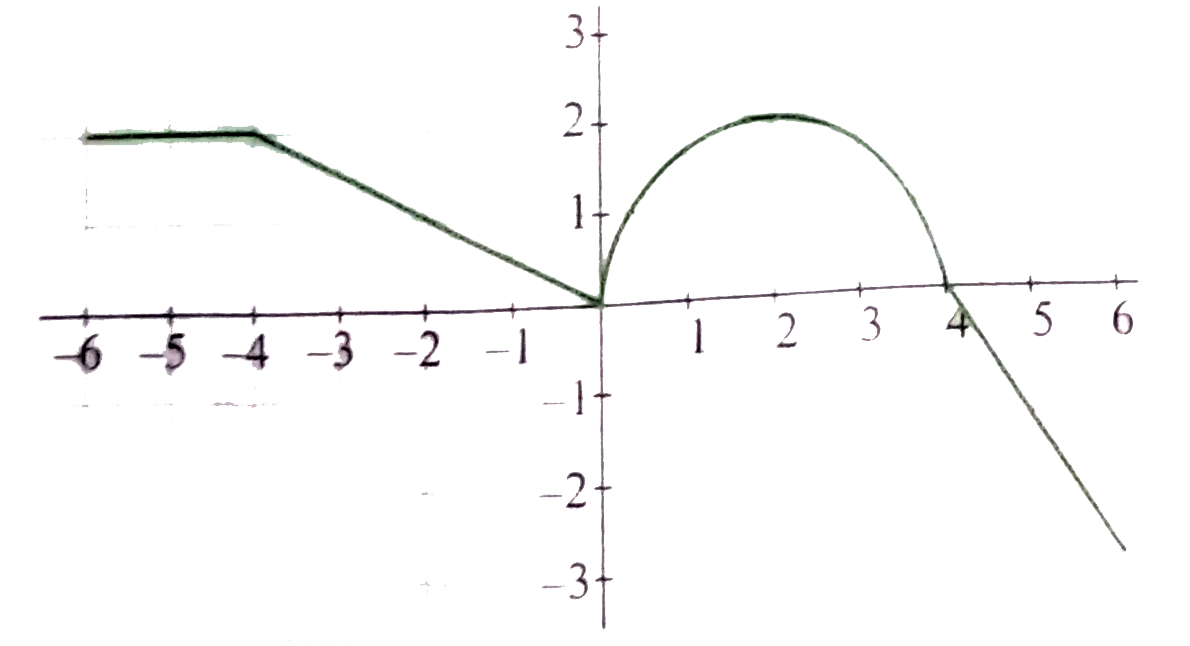
(f) y=f(|x|)
Neglect the graph of y=f(x) for x<0 and take the mirror image of y=f(x) for x>0 about y-axis, keeping y=f(x) for x>0.
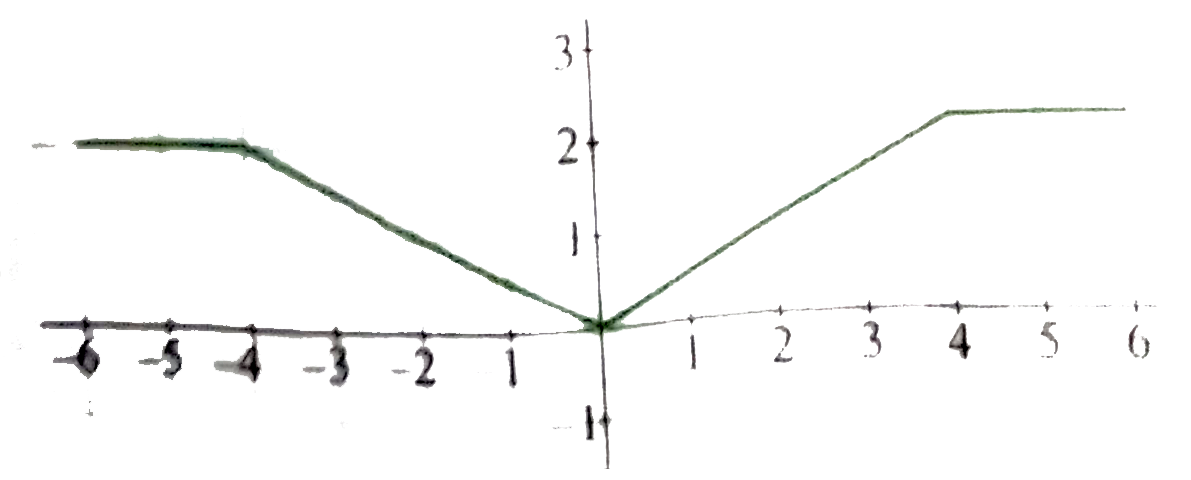
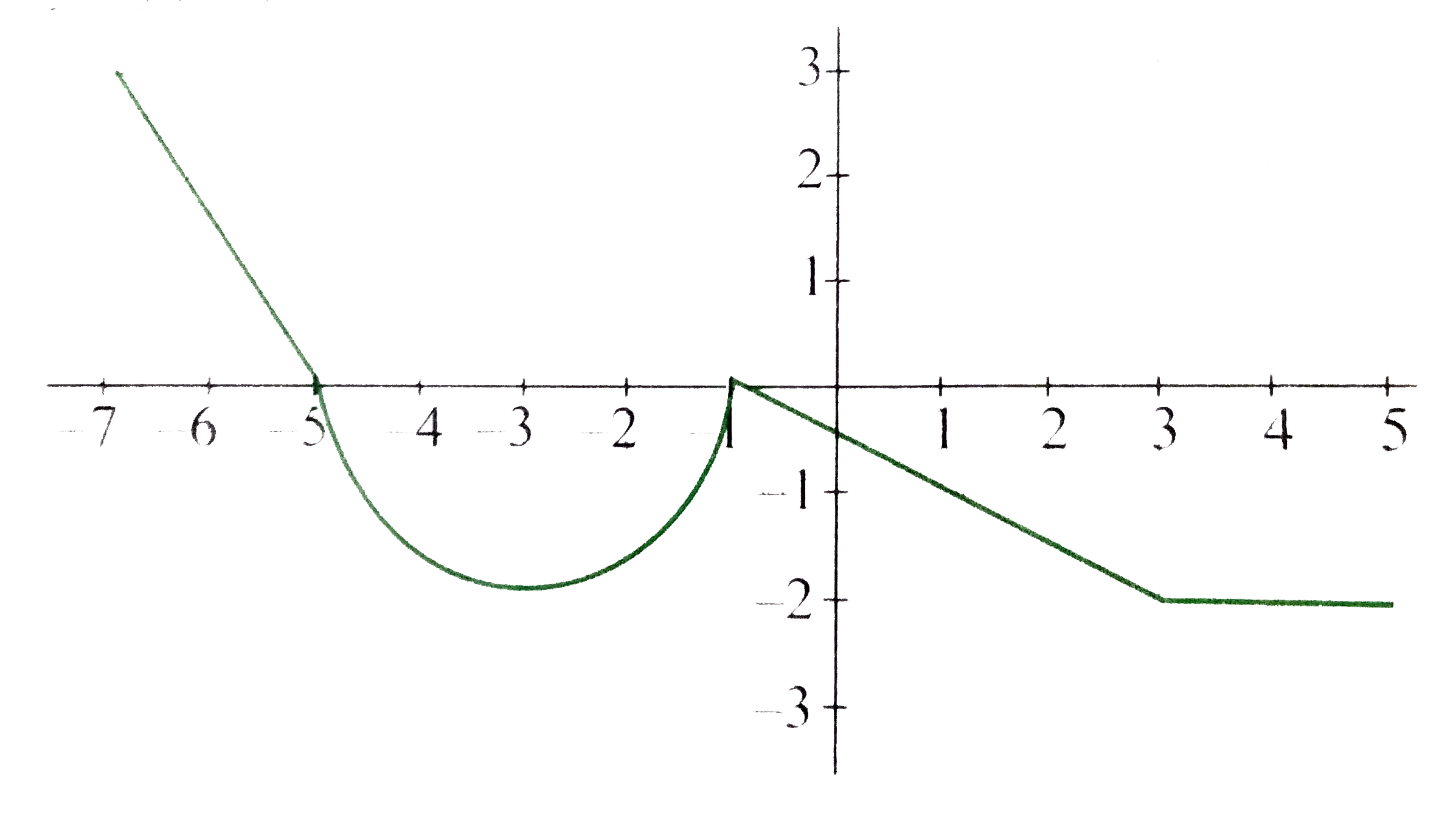
(g) y=f(1−x)
First flip the graph to get y=f(−x) as in (e ). Then shift y=f(−x), 1 unit left hand side to get y=(1−x).
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Single)125videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)27videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.1413videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank31videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isA B
B C
C D
D
Given the graph of y=f(x).

Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)View SolutionGiven the graph of y=f(x), which of the following is graph of y=f(1−x)
View SolutionIf f(x)=sin(πx), then draw the graph of the followings : (i) y=f(|x|) (ii) y=f(−|x|) (iii) |y|=f(x)
View SolutionConsider the function f(x)={2x+3,x≤1and−x2+6,x>1 Then draw the graph of the function y=f(x),y=f(|x|),y=|f(x)|,andy=|f(x)|.
View SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isView SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) isView SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isView Solution

