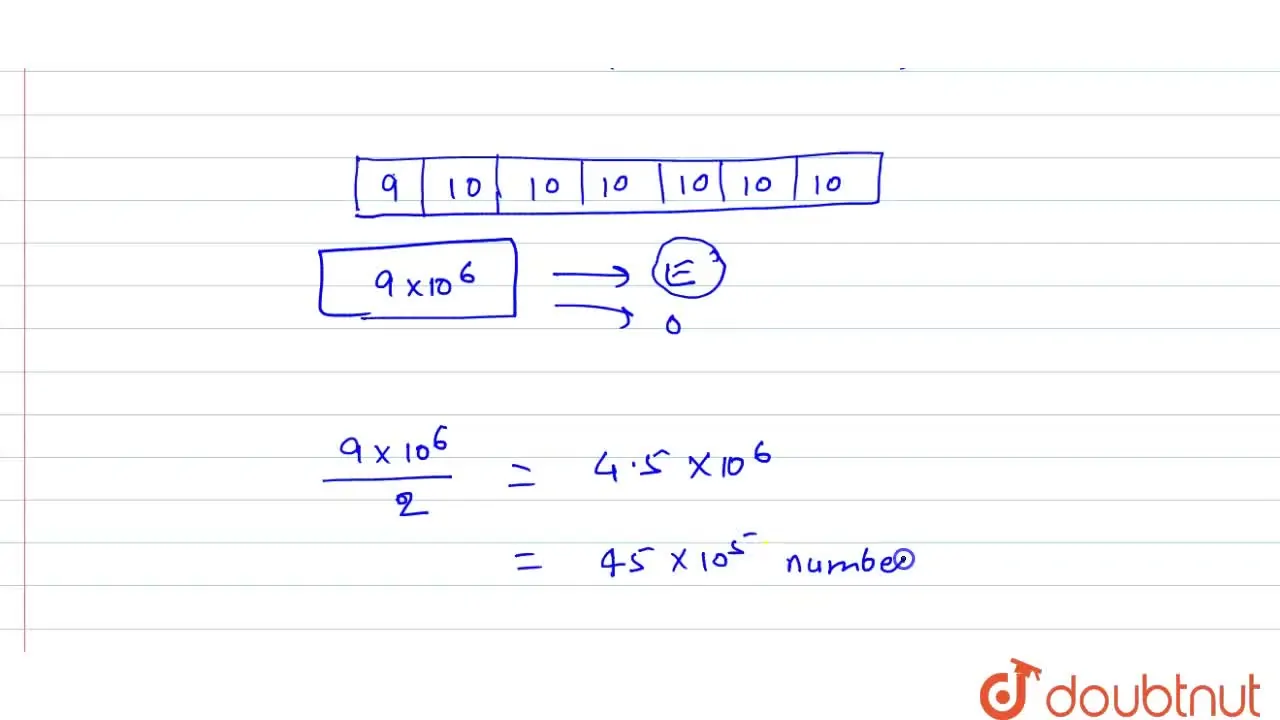
How many different seven digit numbers are there the sum of whose digits is even ?
Let us consider 10 successive seven digit numbers
a1a2a3a4a5a60
a1a2a3a4a5a61
a1a2a3a4a5a62
a1a2a3a4a5a63
…………………….
a1a2a3a4a5a69
Where , a1,a2,a3,........a6 are some digits.
Here we observe that, half of these 10 number i.e., five numbers have an even sum of digits and five numbers have an odd sum of digits . The first digit a1, can assume 9 different values, each of digits a2,a3,a4,a5,a6 can assume 10 different values, the last a7 , can assume only 5 different values for which the sum of all the digits is even.
Hence the required number of different seven digit numbers =9×105×5=45×105.
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Try Yourself65videos
PERMUTATIONS AND COMBINATIONS
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section A Objective type questions (One option is correct )51videos
PERMUTATIONS AND COMBINATIONS
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions3videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)12videos
PRINCIPLE OF MATHEMATICAL
Similar Questions
The total number of seven digit numbers so that the sum of digits is even
View SolutionThe total number of seven digit numbers so that the sum of digits is even
View SolutionNumber of 7 digit numbers the sum of whose digits is 61 is
View SolutionThe total number of seven digit numbers so that the sum of digits is even
View SolutionThe number of 5 digit number such that sum of digits is even
View SolutionFind how many three digit perfect cubes is there whose sum of the digits is a perfect square
View SolutionHow many 3 digit even numbers are there such if 3 is one of the digits then 9 is the next digits ?
View SolutionFind the number of eight-digit numbers the sum of whose digits is 4.
View SolutionHow many four digit numbers are there with distinct digits?
View SolutionHow many 3 digit even numbers are there such if 3 is one of the digits then 9 is the next digits ?
View Solution